题目内容
4.${x^2}-{log_a}(x+1)<2x-1在(\frac{1}{2},1)$内恒成立,则a的取值范围是( )| A. | $[{({\frac{3}{2}})^{-4}},1)$ | B. | $({({\frac{3}{2}})^{-4}},1)$ | C. | $(1,{({\frac{3}{2}})^4})$ | D. | $(1,{({\frac{3}{2}})^4}]$ |
分析 把已知不等式变形,得到x2-2x+1<loga(x+1)在($\frac{1}{2},1$)内恒成立,令f(x)=x2-2x+1,g(x)=loga(x+1),由f($\frac{1}{2}$)=g($\frac{1}{2}$)求得a值,画出两个函数图象,数形结合可得a的取值范围.
解答 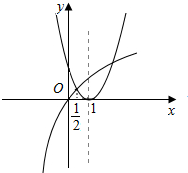 解:由x2-loga(x+1)<2x-1在($\frac{1}{2},1$)内恒成立,得
解:由x2-loga(x+1)<2x-1在($\frac{1}{2},1$)内恒成立,得
x2-2x+1<loga(x+1)在($\frac{1}{2},1$)内恒成立,
令f(x)=x2-2x+1,g(x)=loga(x+1),
作出两个函数的图象如图:
∵f($\frac{1}{2}$)=$\frac{1}{4}$,g($\frac{1}{2}$)=$lo{g}_{a}\frac{3}{2}$,
∴由f($\frac{1}{2}$)=g($\frac{1}{2}$),得$lo{g}_{a}\frac{3}{2}=\frac{1}{4}$,
∴${a}^{\frac{1}{4}}=\frac{3}{2}$,则$a=(\frac{3}{2})^{4}$.
∴要使${x^2}-{log_a}(x+1)<2x-1在(\frac{1}{2},1)$内恒成立,
则a的取值范围是$(1,(\frac{3}{2})^{4}]$.
故选:D.
点评 本题考查函数恒成立问题,考查了数学转化思想方法和数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
15.已知某几何体的正视图和侧视图均如图所示,给出下列5个图形:

其中可以作为该几何体的俯视图的图形个数是( )

其中可以作为该几何体的俯视图的图形个数是( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
19.执行下面的程序框图,则输出的m的值为( )


| A. | 2 | B. | 4 | C. | 5 | D. | 9 |