Question

15．函数$y=2\sqrt{2}sin（ωx+φ）$（其中ω＞0，0＜φ＜π）的图象的一部分如图所示，则（　　）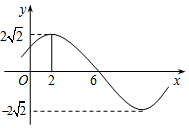

• A． $ω=\frac{π}{8}{，_{\;}}φ=\frac{3π}{4}$
• B． $ω=\frac{π}{8}{，_{\;}}φ=\frac{π}{4}$
• C． $ω=\frac{π}{4}{，_{\;}}φ=\frac{π}{2}$
• D． $ω=\frac{π}{4}{，_{\;}}φ=\frac{3π}{4}$

Answer 1

分析 先利用图象中求得函数的周期，求得ω，最后根据x=2时取最大值，求得φ，即可得解．

解答 解：如图根据函数的图象可得：函数的周期为（6-2）×4=16，
又∵ω＞0，
∴ω=$\frac{2π}{T}$=$\frac{π}{8}$，
当x=2时取最大值，即2$\sqrt{2}$sin（2×$\frac{π}{8}$+φ）=2$\sqrt{2}$，可得：2×$\frac{π}{8}$+φ=2kπ+$\frac{π}{2}$，k∈Z，
∴φ=2kπ+$\frac{π}{4}$，k∈Z，
∵0＜φ＜π，
∴φ=$\frac{π}{4}$，
故选：B．

点评 本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式，考查了学生基础知识的运用和图象观察能力，属于基本知识的考查．