题目内容
6.若实数x,y满足不等式组$\left\{\begin{array}{l}x≥-1\\ x-y≥1\\ x-2y+1≤0\end{array}\right.$,则x+y的最小值是5.分析 画出约束条件的可行域,求出可行域的交点坐标A,然后求解目标函数的最小值即可.
解答 解:作出平面区域,不等式组表示的是一个开放区域(如图5),
当x,y为x-y=1和x-2y+1=0的交点A(3,2),
此时x+y有最小值,所以(x+y)min=5.
故答案为:5.
点评 本题考查线性规划的简单应用,考查数形结合,转化思想的应用.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
11.设各项均为正的等比数列{an}满足a4a8=3a7,则log3(a1a2…a9)等于( )
| A. | 38 | B. | 39 | C. | 9 | D. | 7 |
18.已知函数$f(x)=\left\{\begin{array}{l}lnx,x>1\\{2^{-x+1}},x≤1\end{array}\right.$,若方程$f(x)-ax=\frac{5}{2}$有3个不同的解,则a的取值范围是( )
| A. | $(-∞,-\frac{5}{2}]$ | B. | $(-\frac{5}{2},-\frac{3}{2}]$ | C. | $[-\frac{5}{2},-\frac{3}{2}]$ | D. | $(-\frac{3}{2},+∞)$ |
15.函数$y=2\sqrt{2}sin(ωx+φ)$(其中ω>0,0<φ<π)的图象的一部分如图所示,则( )
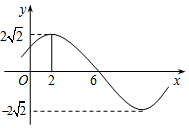

| A. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{3π}{4}$ | B. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{π}{4}$ | C. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{π}{2}$ | D. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{3π}{4}$ |
16.函数y=xlnx的最小值为( )
| A. | -e-1 | B. | -e | C. | e2 | D. | -$\frac{10}{3}$ |
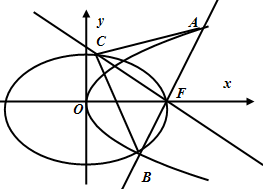 如图,设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是$\frac{\sqrt{3}}{2}$.
如图,设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是$\frac{\sqrt{3}}{2}$.