题目内容
3. 某中学高三年级有400名学生参加月考,用简单随机抽样的方法抽取了一个容量为50的样本,得到数学成绩的频率分布直方图如图所示.
某中学高三年级有400名学生参加月考,用简单随机抽样的方法抽取了一个容量为50的样本,得到数学成绩的频率分布直方图如图所示.(1)求第四个小矩形的高;
(2)估计本校在这次统测中数学成绩不低于120分的人数;
(3)已知样本中,成绩在[140,150]内的有两名女生,现从成绩在这个分数段的学生中随机选取2人做学习交流,求恰好男生女生各有一名的概率.
分析 (Ⅰ)由频率分布直方图,能求出第四个矩形的高.
(Ⅱ)求出成绩不低于120分的频率,由此可估计高三年级不低于120分的人数.
(Ⅲ)由直方图知,成绩在[140,150]的人数是6人,其中女生为A,B,男生为c,d,e,f,利用列举法能求出这6人中抽取2人,其中男生女生各一名的概率.
解答 (本小题满分12分)
解:(Ⅰ)由频率分布直方图,
第四个矩形的高是[1-(0.010+0.012+0.020+0.030)×10]÷10=0.028.…(4分)
(Ⅱ)成绩不低于1(20分)的频率是1-(0.010+0.020)×10=0.7,
可估计高三年级不低于1(20分)的人数为400×0.7=280人.…(7分)
(Ⅲ)由直方图知,成绩在[140,150]的人数是0.012×10×50=6,
记女生为A,B,男生为c,d,e,f,这6人中抽取2人的情况有
AB,Ac,Ad,Ae,Af,Bc,Bd,Be,Bf,cd,ce,cf,de,df,ef,共15种.…(9分)
其中男生女生各一名的有8种,概率为=$\frac{8}{15}$.…(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
11.设各项均为正的等比数列{an}满足a4a8=3a7,则log3(a1a2…a9)等于( )
| A. | 38 | B. | 39 | C. | 9 | D. | 7 |
18.已知函数$f(x)=\left\{\begin{array}{l}lnx,x>1\\{2^{-x+1}},x≤1\end{array}\right.$,若方程$f(x)-ax=\frac{5}{2}$有3个不同的解,则a的取值范围是( )
| A. | $(-∞,-\frac{5}{2}]$ | B. | $(-\frac{5}{2},-\frac{3}{2}]$ | C. | $[-\frac{5}{2},-\frac{3}{2}]$ | D. | $(-\frac{3}{2},+∞)$ |
8.若向量$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(x,4)满足$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数x等于( )
| A. | 8 | B. | -8 | C. | 2 | D. | -2 |
15.函数$y=2\sqrt{2}sin(ωx+φ)$(其中ω>0,0<φ<π)的图象的一部分如图所示,则( )
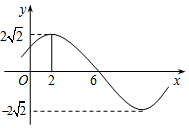

| A. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{3π}{4}$ | B. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{π}{4}$ | C. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{π}{2}$ | D. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{3π}{4}$ |
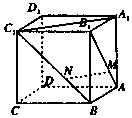 正方体ABCD-A1B1C1D1中,点M、N分别在线段AB1、BC1上,且AM=BN.以下结论:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN与A1C1异面,⑤MN与 A1C1成30°.其中有可能成立的结论的个数为( )
正方体ABCD-A1B1C1D1中,点M、N分别在线段AB1、BC1上,且AM=BN.以下结论:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN与A1C1异面,⑤MN与 A1C1成30°.其中有可能成立的结论的个数为( )