题目内容
4.已知函数f(x)=2x+cosα-2-x+cosα,x∈R,且$f(1)=\frac{{3\sqrt{2}}}{4}$.(1)若0≤α≤π,求α的值;
(2)当m<1时,证明:f(m|cosθ|)+f(1-m)>0.
分析 (1)由f(1),解方程和特殊三角函数值,即可得到;
(2)运用余弦函数的性质和参数分离,结合函数的单调性和奇偶性,即可得证.
解答 解:(1)$f(1)=\frac{{3\sqrt{2}}}{4}$,${2^{1+cosα}}-{2^{-1+cosα}}=\frac{{3\sqrt{2}}}{4}$,
${2^{cosα}}=\frac{{\sqrt{2}}}{2}$…(2分)
$cosα=-\frac{1}{2}$…(3分)
由0≤α≤π,
∴$α=\frac{2π}{3}$…(7分)
(2)证明:∵m<1,若|cosθ|≠1,则$\frac{1}{{1-|{cosθ}|}}≥1$,…(9分)
∴$m<\frac{1}{{1-|{cosθ}|}}$,m(|cosθ|-1)>-1,m|cosθ|>m-1,
又|cosθ|=1时左式也成立,∴m|cosθ|>m-1…(11分)
由(1)知,$f(x)={2^{x-\frac{1}{2}}}-{2^{-x-\frac{1}{2}}}$,在x∈R上为增函数,且为奇函数,…(13分)
∴f(m|cosθ|)>f(m-1)∴f(m|cosθ|)+f(1-m)>0…(15分)
点评 本题考查三角函数的求值和不等式的证明,考查参数分离和运算能力,属于中档题.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
15.函数$y=2\sqrt{2}sin(ωx+φ)$(其中ω>0,0<φ<π)的图象的一部分如图所示,则( )
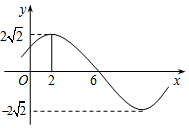

| A. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{3π}{4}$ | B. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{π}{4}$ | C. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{π}{2}$ | D. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{3π}{4}$ |
9.设函数$f(x)=\frac{{{e^2}{x^2}+1}}{x},g(x)=\frac{{{e^2}x}}{e^x}$,对任意x1,x2∈(0,+∞),不等式$\frac{{g({x_1})}}{k}≤\frac{{f({x_2})}}{k+1}$恒成立,则正数k的取值范围是( )
| A. | [1,+∞) | B. | (1,+∞) | C. | $[\frac{1}{2e-1},+∞)$ | D. | $(\frac{1}{2e-1},+∞)$ |
16.函数y=xlnx的最小值为( )
| A. | -e-1 | B. | -e | C. | e2 | D. | -$\frac{10}{3}$ |
