题目内容
1.数列{an}的前n项和为Sn,Sn=(2n-1)an,且a1=1.(1)求数列{an}的通项公式;
(2)若bn=nan,求数列{bn}的前n项和Tn.
分析 (1)将n换为n-1,两式相减,可得{an}是一个以1为首项,$\frac{1}{2}$为公比的等比数列,运用等比数列的通项公式即可得到;
(2)求得bn=nan=n•($\frac{1}{2}$)n-1.再由数列的求和方法:错位相减法,结合等比数列的求和公式即可得到所求和.
解答 解:(1)由${S_n}=({2^n}-1){a_n}$,可得${S_{n-1}}=({2^{n-1}}-1){a_{n-1}}$(n≥2),
两式相减,得${S_n}-{S_{n-1}}=({2^n}-1){a_n}-({2^{n-1}}-1){a_{n-1}}$,
$({2^n}-2){a_n}=({2^{n-1}}-1){a_{n-1}}$,即$\frac{a_n}{{{a_{n-1}}}}=\frac{1}{2}(n≥2)$,
故{an}是一个以1为首项,$\frac{1}{2}$为公比的等比数列,
所以${a_n}={(\frac{1}{2})^{n-1}}$,n∈N*;
(2)bn=nan=n•($\frac{1}{2}$)n-1.
Tn=b1+b2+b3+…+bn=$1×{(\frac{1}{2})^0}+2×{(\frac{1}{2})^1}+3×{(\frac{1}{2})^2}+…+n{(\frac{1}{2})^{n-1}}$,①
$\frac{1}{2}{T_n}$=$1×{(\frac{1}{2})^1}+2×{(\frac{1}{2})^2}+…+(n-1){(\frac{1}{2})^{n-1}}+n{(\frac{1}{2})^n}$,②
①-②,得$\frac{1}{2}{T_n}=1+{(\frac{1}{2})^1}+{(\frac{1}{2})^2}+…+{(\frac{1}{2})^{n-1}}-n{(\frac{1}{2})^n}=2-\frac{n+2}{2^n}$,
所以${T_n}=4-\frac{n+2}{{{2^{n-1}}}}$.
点评 本题考查数列的通项公式的求法,注意运用数列递推式,考查数列的求和方法:错位相减法,考查等比数列的通项公式和求和公式的运用,考查运算能力,属于中档题.

 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案| 时间(分钟) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 次数 | 8 | 14 | 8 | 8 | 2 |
(Ⅰ)若李先生上、下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设ξ是4次使用共享汽车中最优选择的次数,求ξ的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
| A. | (3,6) | B. | (-∞,-2)∪(3,6) | C. | (3,4) | D. | (-∞,-2)∪(3,4) |
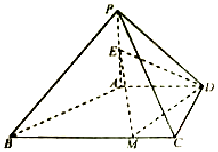 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,AD=DC=PA=2,BC=4,E为PA的中点,M为棱BC上一点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,AD=DC=PA=2,BC=4,E为PA的中点,M为棱BC上一点.