题目内容
13.设集合$A=\left\{{x|{{log}_2}({{x^2}-x-4})>1}\right\}$,$B=\left\{{x|\sqrt{x-2}<2}\right\}$,则A∩B=( )| A. | (3,6) | B. | (-∞,-2)∪(3,6) | C. | (3,4) | D. | (-∞,-2)∪(3,4) |
分析 解不等式求出集合A、B,再计算A∩B.
解答 解:集合$A=\left\{{x|{{log}_2}({{x^2}-x-4})>1}\right\}$
={x|x2-x-4>2}
={x|x<-2或x>3},
$B=\left\{{x|\sqrt{x-2}<2}\right\}$
={x|0≤x-2<4}
={x|2≤x<6},
则A∩B={x|3<x<6}=(3,6).
故选:A.
点评 本题考查了解不等式与集合的运算问题,是基础题.

练习册系列答案
相关题目
3.如表示意某科技公司2012~2016年年利润y(单位:十万元)与年份代号x之间的关系,如果该公司盈利变化规律保持不变,则第n年(以2012年为第1年)年利润的预报值是y=2n2-n.(直接写出代数式即可,不必附加单位)
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年份代号x | 1 | 2 | 3 | 4 | 5 |
| 年利润/十万元 | 1 | 6 | 15 | 28 | 45 |
8.已知关于x的方程x3+ax2+bx+c=0的三个实根分别为一个椭圆,一个抛物线,一个双曲线的离心率,则$\frac{b}{a}$的取值范围( )
| A. | (-1,0) | B. | $(-1,-\frac{1}{2})$ | C. | $(-2,-\frac{1}{2})$ | D. | (-2,+∞) |
5.已知α,β为锐角,且$tanα=\frac{1}{7}$,$cos({α+β})=\frac{{2\sqrt{5}}}{5}$,则cos2β=( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{{7\sqrt{2}}}{10}$ |
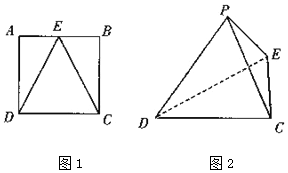 如图1,2,E是正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.
如图1,2,E是正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.