题目内容

12．各项都是正数的数列{an}满足an+1=2an，且a3•a11=16，则a5=（　　）
A．1B．2C．4D．8

分析 由已知条件可求出数列的首项，进而可得所求．

解答 解：由题意可得数列{an}是公比为2的等比数列，
∴a3•a11=a12×212=16，
解得a1=2-4=$\frac{1}{16}$，
∴a5=a1×24=$\frac{1}{16}$×16=1，、
故选：A．

点评 本题考查等比数列的通项公式，求出数列的首项是解决问题的关键，属基础题．

练习册系列答案
相关题目
2．已知f（x）是定义在（0，+∞）上的单调函数，且?x∈（0，+∞），f[f（x）-lnx]=e+1，设a=f（（$\frac{1}{2}$）${\;}^{\frac{1}{3}}$），b=f（（$\frac{1}{3}$）${\;}^{\frac{1}{2}}$），c=f（log2π），则a，b，c的大小关系是c＞a＞b（用“＞”号连接表示）
3．如表示意某科技公司2012～2016年年利润y（单位：十万元）与年份代号x之间的关系，如果该公司盈利变化规律保持不变，则第n年（以2012年为第1年）年利润的预报值是y=2n2-n．（直接写出代数式即可，不必附加单位）
年份20122013201420152016
年份代号x12345
年利润/十万元16152845
20．已知函数$f（x）=sin（{ωx+\frac{π}{6}}）（{0＜ω＜2}）$满足条件：$f（{-\frac{1}{2}}）=0$，为了得到y=f（x）的图象，可将函数g（x）=cosωx的图象向右平移m个单位（m＞0），则m的最小值为（　　）
A．1B．$\frac{1}{2}$C．$\frac{π}{6}$D．$\frac{π}{2}$
7．设点F为抛物线y2=4x的焦点，A，B是抛物线上两点，线段AB的中垂线交x轴于点D（5，0），则|AF|+|BF|=（　　）
A．5B．6C．8D．10
17．已知函数f（x）=lnx+（1-a）x3+bx，g（x）=xex-b（a，b∈R，e为自然对数的底数），且f（x）在点（e，f（e））处的切线方程为y=（$\frac{1}{e}$+1）x
（Ⅰ）求实数a，b的值；
（Ⅱ）求证：f（x）≤g（x）
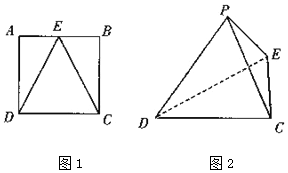4．如图1，2，E是正方形ABCD的AB边的中点，将△AED与△BEC分别沿ED、EC折起，使得点A与点B重合，记为点P，得到三棱锥P-CDE．
（Ⅰ）求证：平面PED⊥平面PCD；
（Ⅱ）求二面角P-CE-D的余弦值．
1．数列{an}的前n项和为Sn，Sn=（2n-1）an，且a1=1．
（1）求数列{an}的通项公式；
（2）若bn=nan，求数列{bn}的前n项和Tn．
2．已知△ABC的外接圆圆心为O，且∠A=60°，若$\overrightarrow{AO}=α\overrightarrow{AB}+β\overrightarrow{AC}（α，β∈R）$，则α+β的最大值为$\frac{2}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网