题目内容
16.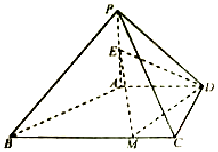 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,AD=DC=PA=2,BC=4,E为PA的中点,M为棱BC上一点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,AD=DC=PA=2,BC=4,E为PA的中点,M为棱BC上一点.(Ⅰ)当BM为何值时,有EM∥平面PCD;
(Ⅱ)在(Ⅰ)的条件下,求点P到平面DEM的距离.
分析 (Ⅰ)取PD中点F,连接EF,CF,推导出四边形EMCF为平行四边形,从而EM∥FC,由此推导出当BM=3时,EM∥平面PCD.
(Ⅱ)设点P到平面DEM的距离为d,由VA-DEM=VE-AMD,能求出点P到平面DEM的距离.
解答 解:(Ⅰ)当BM=3时,有EM∥平面PCD.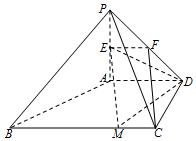
取PD中点F,连接EF,CF,
∵E,F分别为PA,PD的中点,
∴EF∥AD,且$EF=\frac{1}{2}AD=1$.
又∵梯形ABCD中,CM∥AD,且CM=1,
∴EF∥CM,且EF=CM,
∴四边形EMCF为平行四边形,
∴EM∥FC,
又∵EM?平面PCD,FC?平面PCD,∴EM∥平面PCD,
即当BM=3时,EM∥平面PCD.
(Ⅱ)∵E为PA的中点,
∴点P到平面DEM的距离等于点A到平面DEM的距离,设点P到平面DEM的距离为d,
由已知可得,$AM=MD=ED=\sqrt{5}$,$EM=\sqrt{6}$,
∴S△AMD=2,${S_{△DEM}}=\frac{{\sqrt{21}}}{2}$,
由VA-DEM=VE-AMD,得$\frac{1}{3}{S_{△DEM}}•d=\frac{1}{3}{S_{△AMD}}•EA$,
∴$d=\frac{{{S_{△AMD}}•EA}}{{{S_{△DEM}}}}=\frac{{4\sqrt{21}}}{21}$,
所以点P到平面DEM的距离为$\frac{{4\sqrt{21}}}{21}$.
点评 本题考查满足线面平行的点的位置的确定与证明,考查点到平面的距离的求法,考查推理论证能力、运算求解能力、空间思维能力,考查化归转化思想、数形结合思想,是中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
11.已知平面α∩平面β=a,平面β∩平面γ=b,平面γ∩平面α=c,则下列命题:
①若a∥b,则a∥c,b∥c;
②若a∩b=O,则O∈c;
③若a⊥b,b⊥c,则a⊥c.
其中正确的命题是( )
①若a∥b,则a∥c,b∥c;
②若a∩b=O,则O∈c;
③若a⊥b,b⊥c,则a⊥c.
其中正确的命题是( )
| A. | ①②③ | B. | ②③ | C. | ①③ | D. | ①② |
8.已知关于x的方程x3+ax2+bx+c=0的三个实根分别为一个椭圆,一个抛物线,一个双曲线的离心率,则$\frac{b}{a}$的取值范围( )
| A. | (-1,0) | B. | $(-1,-\frac{1}{2})$ | C. | $(-2,-\frac{1}{2})$ | D. | (-2,+∞) |
5.已知α,β为锐角,且$tanα=\frac{1}{7}$,$cos({α+β})=\frac{{2\sqrt{5}}}{5}$,则cos2β=( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{{7\sqrt{2}}}{10}$ |
6.记不等式$\left\{\begin{array}{l}x-y+1≥0\\ 3x-y-3≤0\\ x+y-1≥0\end{array}\right.$所表示的平面区域为D,若对任意(x0,y0)∈D,不等式x0-2y0+c≤0恒成立,则c的取值范围是( )
| A. | (-∞,4] | B. | (-∞,2] | C. | [-1,4] | D. | (-∞,-1] |
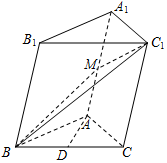 在斜三棱柱ABC-A1B1C1中,AB=AC,平面BB1C1C⊥底面ABC,点M、D分别是线段AA1、BC的中点.
在斜三棱柱ABC-A1B1C1中,AB=AC,平面BB1C1C⊥底面ABC,点M、D分别是线段AA1、BC的中点.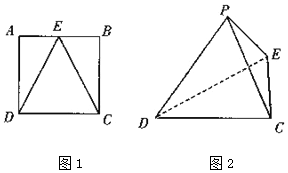 如图1,2,E是正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.
如图1,2,E是正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.