题目内容
6.已知函数f(x)=$\frac{xlnx}{x-1}$.(1)求曲线f(x)在点(e,f(e))(e为自然对数的底数)处的切线方程;
(2)求证:$\frac{\root{2016}{2015}}{\root{2015}{2016}}$>$\frac{2015}{2016}$.
分析 (1)求出原函数的导函数,得到f′(e),再求出f(e),代入直线方程的点斜式得答案;
(2)利用导数证明函数f(x)=$\frac{xlnx}{x-1}$在x>1时为增函数,把要证得不等式两边取自然对数,转化为证明$\frac{2015ln2015}{2015-1}<\frac{2016ln2016}{2016-1}$,则由(1)中的单调性得答案.
解答 (1)解:由f(x)=$\frac{xlnx}{x-1}$,得f′(x)=$\frac{(lnx+1)(x-1)-xlnx}{(x-1)^{2}}$=$\frac{x-lnx-1}{(x-1)^{2}}$,
∴f′(e)=$\frac{e-2}{(e-1)^{2}}$,而f(e)=$\frac{e}{e-1}$,
∴曲线f(x)在点(e,f(e))处的切线方程为y-$\frac{e}{e-1}=\frac{e-2}{(e-1)^{2}}(x-e)$,
整理得:(e-2)x-(e-1)2y+e=0;
(2)证明:要证$\frac{\root{2016}{2015}}{\root{2015}{2016}}$>$\frac{2015}{2016}$,需要证ln$\frac{\root{2016}{2015}}{\root{2015}{2016}}$>ln$\frac{2015}{2016}$,
即证:$\frac{1}{2016}ln2015-\frac{1}{2015}ln2016>ln2015-ln2016$,
也就是证:$\frac{2015ln2015}{2015-1}<\frac{2016ln2016}{2016-1}$,
令g(x)=x-lnx-1,则g′(x)=x-$\frac{1}{x}=\frac{{x}^{2}-1}{x}$,
当x>1时,g′(x)>0,
∴g(x)=x-lnx-1>g(1)=0,
即当x>1时,f′(x)=$\frac{(lnx+1)(x-1)-xlnx}{(x-1)^{2}}$=$\frac{x-lnx-1}{(x-1)^{2}}$>0,
∴函数f(x)=$\frac{xlnx}{x-1}$在x>1时为增函数,则$\frac{2015ln2015}{2015-1}<\frac{2016ln2016}{2016-1}$,
故$\frac{\root{2016}{2015}}{\root{2015}{2016}}$>$\frac{2015}{2016}$.
点评 本题考查利用导数研究过曲线上某点处的切线方程,训练了利用函数单调性证明数列不等式,是中档题.

| A. | 数列{$\frac{{a}_{n}}{{b}_{n}}$}是等比数列,且an=$\frac{2n-1}{{3}^{n}}$ | |
| B. | 数列{$\frac{{a}_{n}}{{b}_{n}}$}是等差数列,且an=$\frac{2n-1}{{3}^{n}}$ | |
| C. | 数列{$\frac{{a}_{n}}{{b}_{n}}$}是等比数列,且an=(2n-1)•3n-1 | |
| D. | 数列{$\frac{{a}_{n}}{{b}_{n}}$}是等差数列,且an=(2n-1)•3n-1 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | [0,1] | B. | [-1,1] | C. | [1,+∞) | D. | (-∞,-1]∪[1,+∞) |
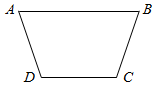 某地修建防洪渠道,其直截面图是等腰梯形ABCD(如图),底CD=40,腰AD=40,为使防洪渠道的通水量最大,应将防洪渠道的上口AB的宽设计为多少?
某地修建防洪渠道,其直截面图是等腰梯形ABCD(如图),底CD=40,腰AD=40,为使防洪渠道的通水量最大,应将防洪渠道的上口AB的宽设计为多少?