题目内容
11.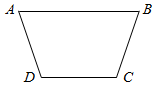 某地修建防洪渠道,其直截面图是等腰梯形ABCD(如图),底CD=40,腰AD=40,为使防洪渠道的通水量最大,应将防洪渠道的上口AB的宽设计为多少?
某地修建防洪渠道,其直截面图是等腰梯形ABCD(如图),底CD=40,腰AD=40,为使防洪渠道的通水量最大,应将防洪渠道的上口AB的宽设计为多少?
分析 设∠A=θ,则梯形的高为40sinθ,下底长为40+80cosθ,求出面积,利用导数的方法求解即可.
解答 解:设∠A=θ,则梯形的高为40sinθ,下底长为40+80cosθ,
所以梯形的面积为:S=$\frac{(40+40+80cosθ)×40sinθ}{2}$=1600(sinθ+sinθcosθ)
求导得S′=1600(cosθ+1)(2cosθ-1)
所以当θ∈(0,$\frac{π}{3}$)时,S>0;当θ∈($\frac{π}{3}$,$\frac{π}{2}$)时,S<0,
所以S在θ=$\frac{π}{3}$时取得极大值,也即最大值,此时AB=80.
点评 本题考查利用数学知识解决实际问题,考查导数知识的运用,正确表示梯形的面积是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.数列{an}的首项a1=2,且(n+1)an=nan+1,则a3的值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
16.已知Sn,Tn分别为数列{$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$}与{$\frac{{2}^{n}+1}{{2}^{n}}$}的前n项和,若Sn>T10+1013,则n的最小值为( )
| A. | 1023 | B. | 1024 | C. | 1025 | D. | 1026 |
3.设函数f(x)=$\left\{\begin{array}{l}{ax+2,x≥2}\\{(\frac{1}{2})^{x}-1,x<2}\end{array}\right.$,对于任意的实数x1≠x2都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立,则实数a的取值范围为( )
| A. | a<0 | B. | a≤0 | C. | a≤-$\frac{11}{8}$ | D. | a<-$\frac{11}{8}$ |
1.已知点O是△ABC的外心,a,b,c分别为角A,B,C的对边,若2c2-c+b2=0,则$\overrightarrow{BC}$•$\overrightarrow{AO}$的最大值是( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{24}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |