题目内容
15.已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=($\frac{1}{2}$)x-1.则不等式f(x)-x2≥0的解集是( )| A. | [0,1] | B. | [-1,1] | C. | [1,+∞) | D. | (-∞,-1]∪[1,+∞) |
分析 设g(x)=f(x)-x2,由题意可得g(x)是定义在R上的偶函数,求出x≥0,不等式f(x)-x2≥0等价于($\frac{1}{2}$)x-1≥x2,可得0≤x≤1,即可解不等式.
解答 解:设g(x)=f(x)-x2,
∵f(x)是定义在R上的偶函数,
∴g(x)是定义在R上的偶函数,
∴x≥0,不等式f(x)-x2≥0等价于($\frac{1}{2}$)x-1≥x2,∴0≤x≤1
∴不等式f(x)-x2≥0的解集为[-1,1].
故选:B.
点评 本题考查了分段函数的应用及函数的性质的应用,属于中档题.

练习册系列答案
相关题目
3.设函数f(x)=$\left\{\begin{array}{l}{ax+2,x≥2}\\{(\frac{1}{2})^{x}-1,x<2}\end{array}\right.$,对于任意的实数x1≠x2都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立,则实数a的取值范围为( )
| A. | a<0 | B. | a≤0 | C. | a≤-$\frac{11}{8}$ | D. | a<-$\frac{11}{8}$ |
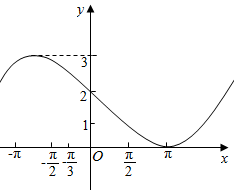 已知函数y=Asin(ωx+φ)+b(A>0,|φ|<π,b为常数)的一段图象(如图所示).
已知函数y=Asin(ωx+φ)+b(A>0,|φ|<π,b为常数)的一段图象(如图所示).