题目内容
定义在R上的奇函数f(x),f(-1)=2,且当x≥0时,f(x)=2x+(a+2)x+b(a,b为常数),则f(-10)的值为 .
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:根据f(0)=0 求得b=-1,根据f(1)=-f(-1)=2,求得a,从而求得函数的解析式,从而求得f(-10)的值.
解答:
解:由题意可得f(0)=1+b=0 b=-1,f(1)=-f(-1)=-2=2+2+a+b,则a=-5.
当x≥0时,f(x)=2x-3x-1,f(-10)=-f(10)=-993,
故答案为:-993.
当x≥0时,f(x)=2x-3x-1,f(-10)=-f(10)=-993,
故答案为:-993.
点评:本题主要考查利用函数的奇偶性求函数的解析式,求函数的值,属于中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
设变量x,y满足约束条件
,其中k>0.若
的最大值为1,则实数k的取值范围是( )
|
| y |
| x |
| A、(1,+∞) |
| B、[1,+∞) |
| C、(0,1] |
| D、(0,1) |
 如图,水平放置的正三棱柱ABC-A1B1C1的主视图是一边长为2的正方形,则该三棱柱的左视图的面积为
如图,水平放置的正三棱柱ABC-A1B1C1的主视图是一边长为2的正方形,则该三棱柱的左视图的面积为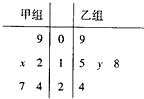 如图方茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为l5,乙组数据的平均数为16.8,则x+y的值为
如图方茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为l5,乙组数据的平均数为16.8,则x+y的值为