题目内容
已知向量
=(2,1),
=(x,y).若x∈{-1,0,1,2},y∈{-1,0,1},求向量
∥
的概率为 .
| a |
| b |
| a |
| b |
考点:古典概型及其概率计算公式,平面向量共线(平行)的坐标表示
专题:概率与统计
分析:先求出基本事件的个数,利用向量平行确定满足
∥
的事件个数,然后代入古典概型概率计算公式求概率;
| a |
| b |
解答:
解:若x∈{-1,0,1,2},y∈{-1,0,1},
则满足条件的
向量共有4×3=12个,
若向量
∥
,则2y-x=0,
故满足条件的
向量共有(0,0),(2,1)两个,
故向量
∥
的概率P=
=
,
故答案为:
则满足条件的
| b |
若向量
| a |
| b |
故满足条件的
| b |
故向量
| a |
| b |
| 2 |
| 12 |
| 1 |
| 6 |
故答案为:
| 1 |
| 6 |
点评:此题考查了古典概型概率计算公式,掌握古典概型概率公式:概率=所求情况数与总情况数之比是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
执行如图的程序框图,输出的结果是( )
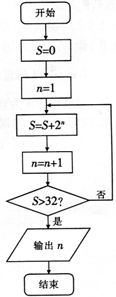

| A、3 | B、4 | C、5 | D、6 |
 如图,AB是圆O的直径,AB=2,D为圆O上一点,过D作圆O的切线交AB的延长线于点C.若DA=DC,则∠BDC=
如图,AB是圆O的直径,AB=2,D为圆O上一点,过D作圆O的切线交AB的延长线于点C.若DA=DC,则∠BDC=