题目内容
设变量x,y满足约束条件
,其中k>0.若
的最大值为1,则实数k的取值范围是( )
|
| y |
| x |
| A、(1,+∞) |
| B、[1,+∞) |
| C、(0,1] |
| D、(0,1) |
考点:简单线性规划
专题:数形结合
分析:不等式组中y-1=k(x-1)对应的直线恒过定点(1,1),通过作可行域可知只有当0<k≤1时,可行域内的点与原点连线的斜率的最大值为1,当k>0时不合题意.
解答:
 解:由约束条件
解:由约束条件
作可行域如图,
∵直线y-1=k(x-1)过定点A(1,1),且k>0,
∴当k最大为1时,可行域内线段AC上的点的坐标满足
最大等于1,
当0<k<1时,可行域内只有A的坐标满足
最大等于1,
当k>1时不合题意.
∴k的取值范围是(0,1].
故选:C.
 解:由约束条件
解:由约束条件
|
∵直线y-1=k(x-1)过定点A(1,1),且k>0,
∴当k最大为1时,可行域内线段AC上的点的坐标满足
| y |
| x |
当0<k<1时,可行域内只有A的坐标满足
| y |
| x |
当k>1时不合题意.
∴k的取值范围是(0,1].
故选:C.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,解答此题的关键是明确
的几何意义,是中档题.
| y |
| x |

练习册系列答案
相关题目
已知全集U={0,1,2,3,4},集合A={1,3,4},B={2,3},则A∩(∁UB)为( )
| A、{3} | B、{0,2} |
| C、∅ | D、{1,4} |
已知等差数列{an}的前n项和为Sn,若S10=
(6x+
)dx,则a3+a8=( )
| ∫ | 2 0 |
| 3 |
| 2 |
| A、3 | B、6 | C、9 | D、12 |
设x0是函数f(x)=x
-3的零点,则x0的值是( )
| 1 |
| 2 |
| A、4 | B、8 | C、9 | D、16 |
执行如图的程序框图,输出的结果是( )
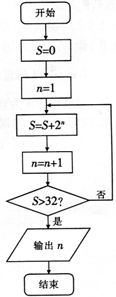

| A、3 | B、4 | C、5 | D、6 |
方程log3x=x-3的根的情况是( )
| A、仅有一个正实数根 |
| B、有两个负根 |
| C、有一个正根和一个负根 |
| D、有两个正根 |
i为虚数,则复数(-1+i)(1+i)=( )
| A、-2+i | B、-2 |
| C、-1+i | D、-1 |