题目内容
12.若y=f(x)是定义在R上周期为2的周期函数,且f(x)是偶函数,当x∈[0,1]时,f(x)=2x-1,则函数g(x)=f(x)-log3(x+1)的零点个数为3.分析 由题意可知,函数f(x)的图象,而要求的是函数g(x)=f(x)-log3(x+1)的零点个数,则问题即是求函数f(x)与y=log3(x+1)的图象的交点个数.
解答 解:由于函数f(x)是定义在R上的偶函数,当x∈[0,1]时,f(x)=2x-1,
则当x∈[-1,0]时,f(x)=2-x-1,
又由函数的周期为2,故可得函数图象,如图示: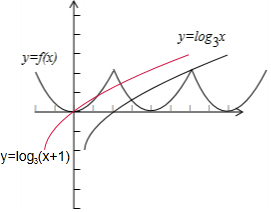
在同一坐标系中,做出函数y=log3(x+1)的图象.
由图知,函数y=f(x)与函数y=log3(x+1)的图象有三个交点
故函数g(x)=f(x)-log3(x+1)的零点个数为3.
故答案为 3.
点评 本题考查函数的零点问题,属于基础题,此类题目常转化为函数图象的交点问题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
3.在△ABC中,a=$\sqrt{3}$b,A=120°,则B的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
20.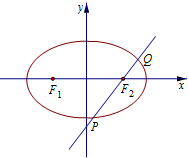 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0),F1,F2分别为椭圆的左,右焦点,如图过F2且斜率为1的直线与椭圆相交于P,Q两点,且$\frac{{|P{F_2}|}}{{|Q{F_2}|}}$=2,则椭圆的离心率e=( )
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0),F1,F2分别为椭圆的左,右焦点,如图过F2且斜率为1的直线与椭圆相交于P,Q两点,且$\frac{{|P{F_2}|}}{{|Q{F_2}|}}$=2,则椭圆的离心率e=( )
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0),F1,F2分别为椭圆的左,右焦点,如图过F2且斜率为1的直线与椭圆相交于P,Q两点,且$\frac{{|P{F_2}|}}{{|Q{F_2}|}}$=2,则椭圆的离心率e=( )
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0),F1,F2分别为椭圆的左,右焦点,如图过F2且斜率为1的直线与椭圆相交于P,Q两点,且$\frac{{|P{F_2}|}}{{|Q{F_2}|}}$=2,则椭圆的离心率e=( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
2.已知F1、F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,P是椭圆上一点,且PF2⊥F1F2,∠PF1F2=$\frac{π}{6}$.则椭圆的离心率是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
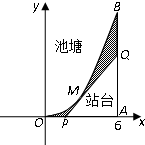 如图,池塘的边缘为曲线段OMB,它可以近似看成是函数f(x)=x2在0≤x≤6的图象,BA垂直于x轴于点A,现要建一个以A为直角的观光站台△APQ,其中斜边PQ与曲线段OMB相切于点M(t,t2),切线PQ交x轴于点P,交线段AB于点Q,图中的阴影部分种植草坪.
如图,池塘的边缘为曲线段OMB,它可以近似看成是函数f(x)=x2在0≤x≤6的图象,BA垂直于x轴于点A,现要建一个以A为直角的观光站台△APQ,其中斜边PQ与曲线段OMB相切于点M(t,t2),切线PQ交x轴于点P,交线段AB于点Q,图中的阴影部分种植草坪. 如图,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2.
如图,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2.