题目内容
12.已知数列{an}的首项为1,Sn为数列{an}的前n项和,Sn+1=qSn+1,其中q>0,n∈N*.(Ⅰ)求证:数列{an}是等比数列;
(Ⅱ)若2a2,a3,a2+2成等差数列,求an的通项公式.
分析 (Ⅰ)由条件利用等比数列的定义和性质,求得数列{an}为首项等于1、公比为q的等比数列,
(Ⅱ)根据2a2,a3,a2+2成等差数列求得公比q的值,可得{an}的通项公式.
解答 解:(Ⅰ)证明:∵Sn+1=qSn+1 ①,
∴当n≥2时,Sn=qSn-1+1 ②,两式相减可得an+1=q•an,
即从第二项开始,数列{an}为等比数列,公比为q.
当n=1时,
∵数列{an}的首项为1,
∴a1+a2=S2=q•a1+1,
∴a2 =a1•q,
∴数列{an}为等比数列,公比为q.
(Ⅱ)∵2a2,a3,a2+2成等差数列,
∴2a3 =2a2+a2+2,∴2q2=2q+q+2,求得q=2,或 q=-$\frac{1}{2}$.
根据q>0,故取q=2,
∴an=2n-1,n∈N*.
点评 本题主要考查等差数列、等比数列的定义和性质,以及数列的递推公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知F1、F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,P是椭圆上一点,且PF2⊥F1F2,∠PF1F2=$\frac{π}{6}$.则椭圆的离心率是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
3.执行如图所示的程序框图,输出的结果为( )


| A. | 1 | B. | e | C. | e2016 | D. | e2017 |
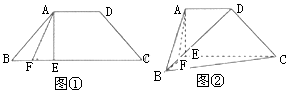 如图①所示,四边形ABCD为等腰梯形,AD∥BC,且AD=$\frac{1}{3}$BC=a,∠BAD=135°,AE⊥BC于点E,F为BE的中点.将△ABE沿着AE折起至△AB′E的位置,得到如图②所示的四棱锥B′-ADCE.
如图①所示,四边形ABCD为等腰梯形,AD∥BC,且AD=$\frac{1}{3}$BC=a,∠BAD=135°,AE⊥BC于点E,F为BE的中点.将△ABE沿着AE折起至△AB′E的位置,得到如图②所示的四棱锥B′-ADCE.