题目内容
6.已知数列{an}满足条件$\frac{1}{3}{a_1}+\frac{1}{3^2}{a_2}+\frac{1}{3^3}{a_3}+…+\frac{1}{3^n}{a_n}=3n+1$,则数列{an}的通项公式为( )| A. | ${a_n}={3^n}$ | B. | ${a_n}={3^{n+1}}$ | ||
| C. | ${a_n}=\left\{\begin{array}{l}12,n=1\\{3^n},n≥2\end{array}\right.$ | D. | ${a_n}=\left\{\begin{array}{l}12,n=1\\{3^{n+1}},n≥2\end{array}\right.$ |
分析 利用数列的递推关系式,直接求解数列的通项公式即可.
解答 解:数列{an}满足条件$\frac{1}{3}{a_1}+\frac{1}{3^2}{a_2}+\frac{1}{3^3}{a_3}+…+\frac{1}{3^n}{a_n}=3n+1$,
可得:$\frac{1}{3}{a}_{1}+\frac{1}{{3}^{2}}{a}_{2}+\frac{1}{{3}^{3}}{a}_{3}+…+\frac{1}{{3}^{n-1}}{a}_{n-1}$=3n-2,(n≥2).
两式作差可得:$\frac{1}{{3}^{n}}$an=3,
可得:an=3n+1,
当n=1时,a1=12,
${a_n}=\left\{\begin{array}{l}12,n=1\\{3^{n+1}},n≥2\end{array}\right.$.
故选:D.
点评 本题考查数列的递推关系式以及通项公式的求法,考查计算能力.

练习册系列答案
相关题目
16.设i是虚数单位,${i^7}-\frac{2}{i}$=( )
| A. | -i | B. | -3i | C. | i | D. | 3i |
17.已知等比数列{an}的首项为a1,公比为q,满足a1(q-1)<0且q>0,则( )
| A. | {an}的各项均为正数 | B. | {an}的各项均为负数 | ||
| C. | {an}为递增数列 | D. | {an}为递减数列 |
1.计算:log29•log38=( )
| A. | 6 | B. | 8 | C. | 10 | D. | 1 |
18.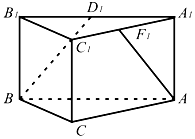 如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )
如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )
 如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )
如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线平行于直线l:3x-2y+3$\sqrt{13}$=0,且双曲线的一个焦点在直线l上,则双曲线方程为( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{5{x}^{2}}{16}$-$\frac{5{y}^{2}}{9}$=1 |