题目内容
用分析法证明：若a＞b＞0，m＞0，则
＞
．
| a |
| b |
| a+m |
| b+m |
考点：综合法与分析法(选修）
专题：证明题
分析：利用分析法，要证
＞
，只需证明m（a-b）＞0，依题意，而该式成立，从而可证得结论．
| a |
| b |
| a+m |
| b+m |
解答：
解：要证明
＞
，∵a＞b＞0，m＞0，
∴只需证明a（b+m）＞b（a+m），
即证am＞bm，即证m（a-b）＞0，该式显然成立，
故结论成立．
| a |
| b |
| a+m |
| b+m |
∴只需证明a（b+m）＞b（a+m），
即证am＞bm，即证m（a-b）＞0，该式显然成立，
故结论成立．
点评：本题考查综合法与分析法证明不等式，突出考查分析法的应用，属于中档题．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
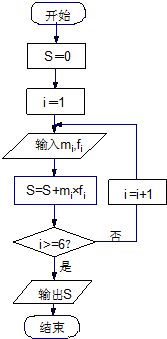“世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”，以提高公众对健康睡眠的自我管理能力和科学认识．为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间（单位：小时），共有2000人参加调查，现将数据整理分组后如题中表格所示．
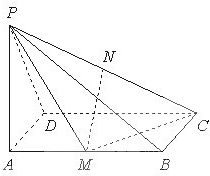如图，已知PA⊥矩形ABCD所在的平面，M、N分别为AB、PC的中点，∠PDA=45°，AB=2，AD=1．
如图所示，△ABC内接于⊙O，AB=AC，直线XY切⊙O于点C，BD∥XY，AC、BD相交于E．
如图，在直三棱柱ABC-A1B1C1中，AC=BC=BB1=2．AB=2