题目内容
设a，b∈R+，现有下列命题：
①若a2-b2=1，则a-b＜1；
②若
-
=1，则a-b＜1；
③若|
-
|=1，则|a-b|＜1；
④若|a2-b2|=1，则|a-b|＜1
其中正确命题的序号为 ．
①若a2-b2=1，则a-b＜1；
②若
| 1 |
| b |
| 1 |
| a |
③若|
| a |
| b |
④若|a2-b2|=1，则|a-b|＜1
其中正确命题的序号为
考点：命题的真假判断与应用
专题：不等式的解法及应用
分析：利用不等式的基本性质即可判断出．
解答：
解：由于a，b∈R+，可得：
①∵a2-b2=1，∴0＜a-b＜a+b，∴a-b=
＜1；
②若
-
=1，则0＜b＜a，取a=10，则b=
，于是a-b=10-
＞1，因此不正确；
③若|
-
|=1，则|a-b|=|
-
| |
+
|=|
+
|＞|
-
|=1，因此不正确；
④若|a2-b2|=1，而|a-b|＜a+b，则|a-b|=
＜1，因此正确．
综上可知：只有①④正确．
故答案为：①④．
①∵a2-b2=1，∴0＜a-b＜a+b，∴a-b=
| 1 |
| a+b |
②若
| 1 |
| b |
| 1 |
| a |
| 10 |
| 11 |
| 10 |
| 11 |
③若|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
④若|a2-b2|=1，而|a-b|＜a+b，则|a-b|=
| 1 |
| a+b |
综上可知：只有①④正确．
故答案为：①④．
点评：本题综合考查了不等式的基本性质，属于中档题．
练习册系列答案
高中必刷题系列答案
相关题目
函数f（x）=
sin2x+cos2x的一条对称轴方程是（ ）
| 3 |
A、x=-
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
如图，在直三棱柱ABC-A1B1C1中，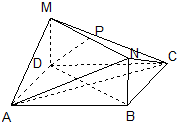
在如图所示的几何体中，四边形ABCD和BDMN都是矩形，且MD⊥平面ABCD，P是MN的中点．若AB=4，BC=3，MD=1，
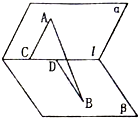如图，在60°的两面角α-l-β中，A∈α，B∈β，AC⊥l与C，BD⊥l于D，AC=2，BD=3，AB=5，则CD=