题目内容
设公比大于零的等比数列{an}的前n项和为Sn,且a1=1,S4=5S2,数列{bn}的前n项和为Tn,满足b1=1,Tn=n2bn,n∈N*.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)满足bn>
对所有的n∈N*均成立,求实数λ的取值范围.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)满足bn>
| λ |
| an |
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件,利用等比数列的前n项和公式能求出公比,由此能求出数列{an}的通项公式;由b1=1,Tn=n2bn,求出Tn-1,由此利用累乘法能求出{bn}的通项公式.
(Ⅱ)设cn=anbn,则cn=
,由此能求出λ的取值范围.
(Ⅱ)设cn=anbn,则cn=
| 2n |
| n(n+1) |
解答:
解:(Ⅰ)∵公比大于零的等比数列{an}的前n项和为Sn,且a1=1,S4=5S2,
即S4=5S2,q>0,
∴
=5×
,
解得q=2,an=2n-1.
∵数列{bn}的前n项和为Tn,满足b1=1,Tn=n2bn,n∈N*.
∴
,
∴
=
(n>1),
∴
•
•
•…•
=
•
•
•…•
•
=
∴bn=
,
当n=1时也满足.
∴bn=
.
(Ⅱ)设cn=anbn,则cn=
,
cn+1-cn=
-
=
=
,
即c1>c2=c3<c4<c5<…
当n=2或3时,cn的最小值是
.
∴λ<
.
即S4=5S2,q>0,
∴
| 1-q4 |
| 1-q |
| 1-q2 |
| 1-q |
解得q=2,an=2n-1.
∵数列{bn}的前n项和为Tn,满足b1=1,Tn=n2bn,n∈N*.
∴
|
∴
| bn |
| bn-1 |
| n-1 |
| n+1 |
∴
| bn |
| bn-1 |
| bn-1 |
| bn-2 |
| bn-2 |
| bn-3 |
| b2 |
| b1 |
| n-1 |
| n+1 |
| n-2 |
| n |
| n-3 |
| n-1 |
| 2 |
| 4 |
| 1 |
| 3 |
| 2 |
| n(n+1) |
∴bn=
| 2 |
| n(n+1) |
当n=1时也满足.
∴bn=
| 2 |
| n(n+1) |
(Ⅱ)设cn=anbn,则cn=
| 2n |
| n(n+1) |
cn+1-cn=
| 2n+1 |
| (n+1)(n+2) |
| 2n |
| n(n+1) |
| 2n+1n-2n(n+2) |
| n(n+1)(n+2) |
=
| 2n(n-2) |
| n(n+1)(n+2) |
即c1>c2=c3<c4<c5<…
当n=2或3时,cn的最小值是
| 2 |
| 3 |
∴λ<
| 2 |
| 3 |
点评:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
设a,b∈R+,现有下列命题:
①若a2-b2=1,则a-b<1;
②若
-
=1,则a-b<1;
③若|
-
|=1,则|a-b|<1;
④若|a2-b2|=1,则|a-b|<1
其中正确命题的序号为 .
①若a2-b2=1,则a-b<1;
②若
| 1 |
| b |
| 1 |
| a |
③若|
| a |
| b |
④若|a2-b2|=1,则|a-b|<1
其中正确命题的序号为
如图是一个算法框图,则输出的k的值是( )


| A、5 | B、6 | C、7 | D、8 |
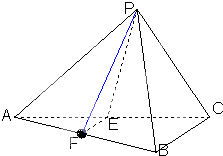 已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.