题目内容
函数f（x）=
sin2x+cos2x的一条对称轴方程是（ ）
| 3 |
A、x=-
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
考点：两角和与差的正弦函数
专题：三角函数的图像与性质
分析：利用两角和的正弦公式化简函数f（x）的解析式为2sin（2x+
），令2x+
=kπ+
，k∈z，求得x的值，可得函数的一条对称轴方程．
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
解答：
解：函数f（x）=
sin2x+cos2x=2sin（2x+
），
令2x+
=kπ+
，k∈z，求得x=
+
，k∈z，
故函数的一条对称轴方程为x=
+
=
，
故选：D．
| 3 |
| π |
| 6 |
令2x+
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 6 |
故函数的一条对称轴方程为x=
| π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
故选：D．
点评：本题主要考查两角和的正弦公式，正弦函数的图象的对称性，属于中档题．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
下列有关命题的说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” |
| B、若p∨q为真命题，则p、q均为真命题． |
| C、命题“存在x∈R，使得x2+x+1＜0”的否定是：“对任意x∈R，均有x2+x+1＜0” |
| D、命题“若x=y，则sinx=siny”的逆否命题为真命题 |
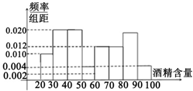道路安全交通法规定，驾驶员血液酒精含量在20～80mg/100ml，属酒后驾车，血液酒精含量在80mg/100ml以上时，属醉酒驾车，2011年6月1日7：00至22：30，某地查处酒后驾车和醉酒驾车共50起，如图是对这50人的血液中酒精含量进行检测所得结果的频率分布直方图，则属于醉酒驾车的人数大约为（ ）已知集合A={x|2x2+7x-15＜0}，B={x|x2+ax+b≤0}，若A∩B=∅，A∪B={x|-5＜x≤2}，则实数a，b的值分别是（ ）
| A、2，4 | ||
B、
| ||
C、
| ||
D、-
|