题目内容
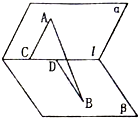如图，在60°的两面角α-l-β中，A∈α，B∈β，AC⊥l与C，BD⊥l于D，AC=2，BD=3，AB=5，则CD=考点：点、线、面间的距离计算
专题：空间向量及应用
分析：由题设知
=
+
+
，由此利用向量法能求出CD的长度．
| AB |
| AC |
| CD |
| DB |
解答：
AC解：∵AC⊥l，BD⊥l，α-l-β为60°的二面角，
∴＜
，
＞=60°，
∵
=
+
+
，?∴
2=
2+
2+
2+2
•
+2
•
+2
•
．?
∴52=22+
2+32+2•|
||
|•cos＜
，
＞，?
∴
2=12-2×2×3×cos120°=18．?
∴CD的长度为3
．
故答案为：3
．
∴＜
| AC |
| BD |
∵
| AB |
| AC |
| CD |
| DB |
| AB |
| AC |
| CD |
| DB |
| AC |
| CD |
| AC |
| DB |
| CD |
| DB |
∴52=22+
| CD |
| AC |
| DB |
| AC |
| DB |
∴
| CD |
∴CD的长度为3
| 2 |
故答案为：3
| 2 |
点评：本题考查线段落长的求法，是中档题，解题时要注意向量法的合理运用．
练习册系列答案
相关题目
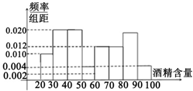道路安全交通法规定，驾驶员血液酒精含量在20～80mg/100ml，属酒后驾车，血液酒精含量在80mg/100ml以上时，属醉酒驾车，2011年6月1日7：00至22：30，某地查处酒后驾车和醉酒驾车共50起，如图是对这50人的血液中酒精含量进行检测所得结果的频率分布直方图，则属于醉酒驾车的人数大约为（ ）
如图，已知椭圆Γ：设a，b∈R+，现有下列命题：
①若a2-b2=1，则a-b＜1；
②若
-
=1，则a-b＜1；
③若|
-
|=1，则|a-b|＜1；
④若|a2-b2|=1，则|a-b|＜1
其中正确命题的序号为 ．
①若a2-b2=1，则a-b＜1；
②若
| 1 |
| b |
| 1 |
| a |
③若|
| a |
| b |
④若|a2-b2|=1，则|a-b|＜1
其中正确命题的序号为
甲、乙两个学习小组各有10名同学，他们在一次数学测验中成绩的茎叶图（如图），则他们在这次测验中成绩较好的是
按照如图的程序框图执行，若输出结果为31，则M处的条件为（ ）| A、k≥32 | B、k＜16 |
| C、k＜32 | D、k≥16 |