题目内容
13.已知函数f(x)=|x+1|+2|x-a2|(a∈R).(1)若函数f(x)的最小值为3,求a的值:
(2)在(1)的条件下,若直线y=m与函数y=f(x)的图象围成一个三角形,求m的范围,并求围成的三角形面积的最大值.
分析 (1)分类讨论以去掉绝对值号,从而确定函数的单调性,从而可得f(a2)=a2+1=3,从而求得;
(2)化简f(x)=|x+1|+2|x-2|,从而作出函数的图象,结合图象求解.
解答 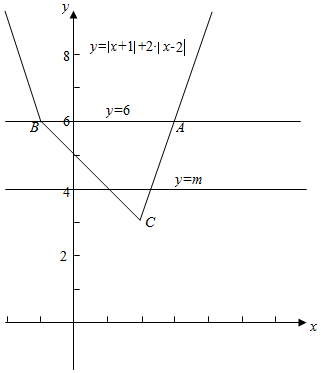 解:(1)当x≥a2时,
解:(1)当x≥a2时,
f(x)=x+1+2x-2a2=3x-2a2+1,
当-1<x<a2时,
f(x)=x+1+2a2-2x=-x+2a2+1,
当x≤-1时,
f(x)=-x-1+2a2-2x=-3x+2a2-1,
故f(x)在(∞,a2)上是减函数,在(a2,+∞)上是增函数;
故f(a2)=a2+1=3,
故a2=2,
故a=$\sqrt{2}$或a=-$\sqrt{2}$;
(2)由(1)知,f(x)=|x+1|+2|x-2|,
由题意作图如下,
,
结合图象可知,A(3,6),B(-1,6),C(2,3);
故3<m≤6,
且m=6时面积最大为$\frac{1}{2}$×(3+1)×3=6.
点评 本题考查了绝对值函数的应用及数形结合的思想方法应用,属于中档题.

练习册系列答案
相关题目
1.下列结论中正确的是( )
①α∥β,β∥γ,则α∥γ;
②过平面外一条直线有且只有一个平面与已知平面平行;
③平面外的两条平行线中,如果有一条和平面平行,那么另一条也和这个平面平行;
④如果一条直线与两个平行平面中一个相交,那么它与另一个必相交.
①α∥β,β∥γ,则α∥γ;
②过平面外一条直线有且只有一个平面与已知平面平行;
③平面外的两条平行线中,如果有一条和平面平行,那么另一条也和这个平面平行;
④如果一条直线与两个平行平面中一个相交,那么它与另一个必相交.
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②③④ |
3.函数f(x)=sin4x+acos4x图象的一条对称轴方程是直线x=$\frac{π}{6}$,则a=( )
| A. | 1 | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
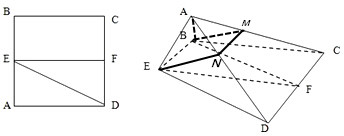 已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.
已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.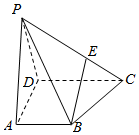 如图,四棱锥P-ABCD的底面ABCD是梯形,AB∥CD,且AB=$\frac{2}{3}$CD,试问在PC上能否找到一点E,使得BE∥平面PAD?若能,请确定点E的位置,并给出证明;若不能,请说明理由.
如图,四棱锥P-ABCD的底面ABCD是梯形,AB∥CD,且AB=$\frac{2}{3}$CD,试问在PC上能否找到一点E,使得BE∥平面PAD?若能,请确定点E的位置,并给出证明;若不能,请说明理由.