题目内容
5.若x5=an+a1(x-1)+a2(x-1)2+a3(x-1)3+a4(x-1)4+a5(x-1)5,则a4=5.分析 根据[1+(x-1)]5=an+a1(x-1)+a2(x-1)2+a3(x-1)3+a4(x-1)4+a5(x-1)5,利用二项展开式的通项公式,求得a4的值.
解答 解:∵x5=[1+(x-1)]5=an+a1(x-1)+a2(x-1)2+a3(x-1)3+a4(x-1)4+a5(x-1)5,
∴a4=${C}_{5}^{4}$=5,
故答案为:5.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
16.计算$\frac{1+i}{i}$+(2-i)2等于( )
| A. | 4-5i | B. | 3-4i | C. | 5-4i | D. | 4-3i |
10.已知集合A={x|$\frac{x-2}{x+1}$<0},B={x||x|<a},则“a=1”是“B⊆A”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知函数f(x)(x∈R),满足f(-x)=-f(x),f(3-x)=f(x),则f(435)=( )
| A. | 0 | B. | 3 | C. | -3 | D. | 不确定 |
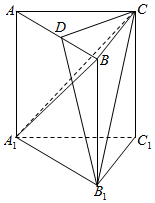 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.