题目内容
4.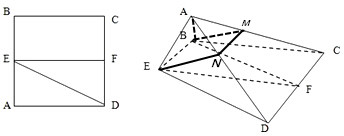 已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.
已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.(1)证明:BF∥平面ADE;
(2)若过BE的截面与平面ACD交于MN,求证:CD∥MN.
分析 (1)由已知推导出四边形EBFD是平行四边形,从而BF∥ED,由此能证明BF∥平面ADE.
(2)推导出BE∥平面ACD,BE∥MN,再由BE∥CD,能证明CD∥MN.
解答 证明:(1)E、F分别是正方形ABCD的边AB、CD的中点
∴EB∥FD,且EB=FD,
∴四边形EBFD是平行四边形,
∴BF∥ED,
∵BD?平面AED,而BF?平面AED,
∴BF∥平面ADE.
(2)∵过BE的截面与平面ACD交于MN,EB∥FD,
BE?平面ACD,CD?平面ACD,
∴BE∥平面ACD,∵MN?平面ACD,∴BE与MN无公共点,
∵BE?平面BENM,MN?平面BENM,
∴BE∥MN,
∵BE∥CD,∴CD∥MN.
点评 本题考查线面平行的证明,考查线线平行的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
16.计算$\frac{1+i}{i}$+(2-i)2等于( )
| A. | 4-5i | B. | 3-4i | C. | 5-4i | D. | 4-3i |