题目内容
3.已知等比数列{an}和等差数列{bn}均是首项为1的递增数列,且a2=b2,a3=b4.(I)求数列{an}和{bn}的通项公式;
(Ⅱ)若数列{cn}满足cn=an+(-1)nbn,求数列{cn)前n项和Sn.
分析 (I)利用等差数列与等比数列的通项公式即可得出.
(II)cn=an+(-1)nbn=2n-1+(-1)n•n.对n分类讨论,分求和,利用等比数列的前n项和公式即可得出.
解答 解:(I)设等比数列{an}的公比为q,等差数列{bn}的公差为d>0,∵a2=b2,a3=b4.
∴q=1+d,q2=1+3d,解得q=2,d=1.
∴an=2n-1,bn=1+(n-1)=n.
(II)cn=an+(-1)nbn=2n-1+(-1)n•n.
∴n=2k(k∈N*)时,数列{cn)前n项和Sn=S2k=$\frac{{2}^{n}-1}{2-1}$+(2-1)+(4-3)+…+[n-(n-1)]=2n-1+k=2n-1+$\frac{n}{2}$.
n=2k-1时,Sn=S2k-1=$\frac{{2}^{n}-1}{2-1}$-1+(2-3)+(4-5)+…+[(n-1)-n)]=2n-1-1-(k-1)=2n-1-$\frac{n+1}{2}$=2n-$\frac{n+3}{2}$.
∴Sn=$\left\{\begin{array}{l}{{2}^{n}-1+\frac{n}{2},n=2k}\\{{2}^{n}-\frac{n+3}{2},n=2k-1}\end{array}\right.$(k∈N*).
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、分类讨论方法、分组求和,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.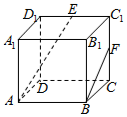 如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )
如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )
 如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )
如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )| A. | -$\frac{{5\sqrt{6}}}{18}$ | B. | -$\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{6}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
11.设向量$\overrightarrow a$=(1,x),$\overrightarrow b$=(x,4),则“x=$\int_{1}^{e}{\frac{2}{t}}$dt”(e=2.718…是自然对数的底数)是“$\overrightarrow a$∥$\overrightarrow b$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.等差数列{an}中,a3+a4+a8=12,则前9项和S9=( )
| A. | 18 | B. | 24 | C. | 36 | D. | 48 |