题目内容
在棱长为1的正方体内,有两球相外切,并且又分别与正方体内切.
(1)以正方体每个面的中心为顶点构成一个八面体,求该八面体的体积.
(2)求两球半径之和.
(3)球的半径是多少时,两球体积之和最小?
(1)以正方体每个面的中心为顶点构成一个八面体,求该八面体的体积.
(2)求两球半径之和.
(3)球的半径是多少时,两球体积之和最小?
考点:球内接多面体,球的体积和表面积
专题:综合题,空间位置关系与距离
分析:(1)八面体分成两个正四棱锥,求出底面面积,然后求出体积即可.
(2)利用ABCD为过球心的对角面,即可求两球半径之和.
(3)表示出两球的体积之和,利用配方法,求两球体积之和最小.
(2)利用ABCD为过球心的对角面,即可求两球半径之和.
(3)表示出两球的体积之和,利用配方法,求两球体积之和最小.
解答:
解:(1)将正方体的六个面的中心连接起来,构成一个八面体,分成两个正四棱锥,底面面积为:
,高为
,一个正四棱锥的体积为:
×
×
=
,
所以这个八面体的体积是V=
;
(2)如图,ABCD为过球心的对角面,AC=
,
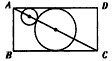
设两球半径为R、r,则有R+r+
(R+r)=
,
所以R+r=
;
(2)设两球的体积之和为V,
则V=
π(R3+r3)=
π•
[3R2-
R+(
)2],
所以当R=
时,V有最小值.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 12 |
所以这个八面体的体积是V=
| 1 |
| 6 |
(2)如图,ABCD为过球心的对角面,AC=
| 3 |

设两球半径为R、r,则有R+r+
| 3 |
| 3 |
所以R+r=
3-
| ||
| 2 |
(2)设两球的体积之和为V,
则V=
| 4 |
| 3 |
| 4 |
| 3 |
3-
| ||
| 2 |
3(3-
| ||
| 2 |
3-
| ||
| 2 |
所以当R=
3-
| ||
| 4 |
点评:本题是基础题,考查棱锥的体积的求法,正方体的内接体的知识,解题关键在八面体转化为两个正四棱锥,是常考题型.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
“a=1”是“复数a2-1+(a+1)i(a∈R,i为虚数单位)是纯虚数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
sin(-660°)=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
一个正四棱柱的各个顶点都在一个半径为2cm的球面上,如果正四棱柱的底面边长为2cm,那么该棱柱的表面积为( )
A、(2+4
| ||
B、(4+8
| ||
C、(8+16
| ||
D、(16+32
|
 已知在平面直角坐标系中,坐标原点为O,点A,B在x轴上,OA=1,OB=5,点C在y轴上,OC=2.5,第一象限有一点D的坐标为(3,4),连接AD,BD,点E是线段AB上一动点(不与点A重合),过E作EF⊥AB交射线AD于点F,以EF为一边在EF的右侧作正方形EFGH,设E点的坐标为(t,0)
已知在平面直角坐标系中,坐标原点为O,点A,B在x轴上,OA=1,OB=5,点C在y轴上,OC=2.5,第一象限有一点D的坐标为(3,4),连接AD,BD,点E是线段AB上一动点(不与点A重合),过E作EF⊥AB交射线AD于点F,以EF为一边在EF的右侧作正方形EFGH,设E点的坐标为(t,0)