题目内容
15.下列说法中正确的是( )| A. | 若p∨q为真命题,则p,q均为真命题 | |
| B. | “a≥5”是“?x∈[1,2],x2-a≤0恒成立“的充要条件 | |
| C. | 在△ABC中,“a>b”是“sinA>sinB”的必要不充分条件 | |
| D. | 命题“?x0∈R,2x0≤0”的否定是“?x∈R,2x>0” |
分析 利用或命题的真假判断A的正误;充要条件判断B的正误;三角形的边角关系判断C的正误;命题的否定判断D的正误;
解答 解:对于A,若p∨q为真命题,一真为真,说p,q均为真命题,是不正确的;
对于B,“a≥5”是“?x∈[1,2],x2-a≤0恒成立“的充要条件,充分条件成立,必要条件是a≥4,所以B正确;
对于C,在△ABC中,“a>b”?“sinA>sinB”的充分必要条件,所以C不正确;
对于D,命题“?x0∈R,2x0≤0”的否定是“?x∈R,2x>0”,满足命题的否定形式,正确.
故选:D.
点评 本题考查命题的真假的判断与应用,充要条件的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
6.非空集A={x|2a+1≤x≤3a-5},B=$\{x|y=\sqrt{(3-x)(x-22)}\}$,则A⊆A∩B的一个充分不必要条件是( )
| A. | 1≤a≤9 | B. | 6<a<9 | C. | 6≤a≤9 | D. | a≤9 |
3.若cosα=$\frac{1}{2}$,α∈(0,π),则cos($\frac{π}{2}$-α)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
4.已知a=2${\;}^{\frac{4}{3}}$,b=3${\;}^{\frac{2}{3}}$,c=2.5${\;}^{\frac{1}{3}}$,则( )
| A. | a<b<c | B. | c<b<a | C. | b<c<a | D. | c<a<b |
5.若角α的终边经过点P(-1,3),则tanα的值为( )
| A. | $-\frac{1}{3}$ | B. | -3 | C. | $-\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
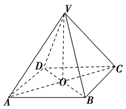 如图所示,四棱锥V-ABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.
如图所示,四棱锥V-ABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.