题目内容
在(2x-3y+z)5展开式中,x2yz2的系数为( )
| A、360 | B、180 |
| C、-360 | D、-180 |
考点:二项式定理的应用
专题:二项式定理
分析:先按[(2x+z)-3y]5二项式展开,求出通项中含有y的项,再求二项式(2x+z)4的展开式中含有x2z2的项,从而求出x2yz2的系数.
解答:
解:∵(2x-3y+z)5=[(2x+z)-3y]5,
∴二项式展开式的通项是Tr+1=
•(2x+z)5-r•(-3y)r;
令r=1,则T2=
•(2x+z)4•(-3y)=-3×5×(2x+z)4y,
∴二项式(2x+z)4的展开式的通项是:Tr+1=
•(2x)4-r•zr,
令r=2,则T3=
•(2x)2•z2=4×6x2z2;
∴x2yz2的系数为-3×5×4×6=-360.
故选:C.
∴二项式展开式的通项是Tr+1=
| C | r 5 |
令r=1,则T2=
| C | 1 5 |
∴二项式(2x+z)4的展开式的通项是:Tr+1=
| C | r 4 |
令r=2,则T3=
| C | 2 4 |
∴x2yz2的系数为-3×5×4×6=-360.
故选:C.
点评:本题考查了二项式定理的应用问题,解题时应灵活应用二项展开式的通项公式,是基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
圆x2+y2-4y-1=0的圆心和半径是( )
| A、C(2,0),r=5 | ||
B、C(0,2),r=
| ||
C、C(0,-2),r=
| ||
| D、C(-2,0),r=5 |
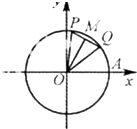 如图,P,Q是以原点为圆心的单位圆上的两个动点,若它们同时从点A(1,0)出发,沿逆时针方向作匀角速度运动,其角速度分别为
如图,P,Q是以原点为圆心的单位圆上的两个动点,若它们同时从点A(1,0)出发,沿逆时针方向作匀角速度运动,其角速度分别为