题目内容
15.双曲线x2-y2=a(a≠0)的渐近线方程为y=±x.分析 双曲线x2-y2=a(a≠0)的渐近线方程为x2-y2=0,由此能求出结果.
解答 解:x2-y2=a(a≠0)的渐近线方程为x2-y2=0,
整理,得y=±x.
故答案为:y=±x.
点评 本题考查双曲线的渐近线方程的求法,是基础题,解题时要认真审题,注意双曲线的简单性质的灵活运用.

练习册系列答案
相关题目
6.已知四面体ABCD的侧面展开图如图所示,则其体积为( )
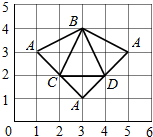

| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
20.对于满足|f(n+1)-f(n)|≤($\frac{1}{10}$)n(n∈N)的所有f(n),若f(0)=1,则f(10)的值所在的区间一定是( )
| A. | (-1,1) | B. | (0,2) | C. | (-$\frac{1}{9}$,$\frac{19}{9}$) | D. | (-$\frac{1}{5}$,$\frac{9}{5}$) |
7.若函数f(x)=a|x+b|(a>0且a≠1,b∈R)是偶函数,则下面的结论正确的是( )
| A. | f(b-3)<f(a+2) | B. | f(b-3)>f(a+2) | ||
| C. | f(b-3)=f(a+2) | D. | f(b-3)与f(a+2)的大小无法确定 |
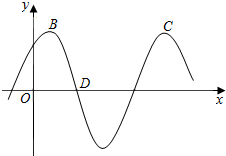 如图所示,B,C两点是函数f(x)=Asin(2x+$\frac{π}{3}$)(A>0)图象上相邻的两个最高点,D点为函数f(x)图象与x轴的一个交点.
如图所示,B,C两点是函数f(x)=Asin(2x+$\frac{π}{3}$)(A>0)图象上相邻的两个最高点,D点为函数f(x)图象与x轴的一个交点.