题目内容

已知各项均为正数的等比数列{an}中，a1a2a3=5，a7a8a9=10，则a4a5a6=（　　）
A、4
2
B、5
2
C、6
D、7
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：由等比数列的性质知，a1a2a3，a4a5a6，a7a8a9成等比数列，即可得出结论．
解答： 解：由等比数列的性质知，a1a2a3，a4a5a6，a7a8a9成等比数列，
所以a4a5a6=5
2
．
故选：B．
点评：本小题主要考查等比数列的性质、指数幂的运算等知识，着重考查了转化与化归的数学思想．
练习册系列答案
相关题目
等差数列{an}中，a3+a7=25，则a2+a4+a6+a8=
 
．
已知在棱长为1的正方体ABCD-A1B1C1D1中，点M、N、P分别是棱AB、BC、AA1的中点，给出下列五个结论：
①AC⊥PM；
②B1D∥PMN；
③AC∥平面PMN；
④过P、M、N的平面截该正方体所得的截面面积为
3
3
4
；
⑤B1P⊥平面PMN．
以上结论中正确的是
 
．（写出所有正确结论的序号）
△ABC中，tanA，tanB是3x2+8x-1=0的两个实数根，则4sin2C-3sinCcosC-5cos2C=
 
．
已知向量|
a
|=
3
，|
b
|=2，
a
与
b
的夹角为30°，则
a
•
b
=
 
．
“龟兔赛跑”讲述了这样的故事：领先的兔子看着缓缓爬行的乌龟，骄傲起来，睡了一觉．当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到了终点．用S1和S2分别表示乌龟和兔子经过时间t所行的路程，则下列图象中与故事情节相吻合的是（　　）
A、
B、
C、
D、
已知函数f（x）=
-
1
3
x+
1
6
，x∈[0，
1
2
]
2x3
x+1
，x∈(
1
2
，1]
，函数g（x）=asin（
π
6
x）-2a+2（a＞0），若存在x1，x2∈[0，1]，使得f（x1）=g（x2）成立，则实数a的取值范围是（　　）
A、[-
2
3
，1]
B、[
1
2
，
4
3
]
C、[
4
3
，
3
2
]
D、[
1
3
，2]
函数f（x）=
x2
x-1
+lg（10-x）的定义域为（　　）
A、R
B、[1，10]
C、（-∞，-1）∪（1，10）
D、（1，10）
已知函数f（x）的图象如图所示，则f（x）的解析式可以为（　　）
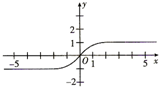
A、f（x）=x 
1
3
B、f（x）=
ln(x+1)，x≥0
ln
1
1-x
，		x＜0
C、f（x）=
ex-e-x
ex+e-x
D、f（x）=
cosx
sinx

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网