题目内容
等差数列{an}中，a3+a7=25，则a2+a4+a6+a8= ．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：根据等差数列的性质所有下标之和相同的两项之和相等，即可得出结论．
解答：
解：等差数列{an}中，
∵a3+a7=25，
∴a2+a4+a6+a8
=2（a3+a7）
=2×25=50．
故答案为：50．
∵a3+a7=25，
∴a2+a4+a6+a8
=2（a3+a7）
=2×25=50．
故答案为：50．
点评：本题考查学生灵活运用等差数列的性质化简求值，考查学生的计算能力，是一道基础题．
练习册系列答案
相关题目
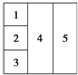如图，用4种不同的颜色对图中5个区域涂色（ 4种颜色全部使用 ），要求每个区域涂一种颜色，相邻的区域不能涂相同的颜色，则不同的涂色方法有已知各项均为正数的等比数列{an}中，a1a2a3=5，a7a8a9=10，则a4a5a6=（ ）
A、4
| ||
B、5
| ||
| C、6 | ||
| D、7 |