题目内容
已知向量|
|=
,|
|=2,
与
的夹角为30°,则
•
= .
| a |
| 3 |
| b |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:依据向量的数量积的定义计算.
解答:
解:∵向量|
|=
,|
|=2,
与
的夹角为30°,则
•
=|
||
|cos30°=
×2×
=3;
故答案为:3.
| a |
| 3 |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 3 |
| ||
| 2 |
故答案为:3.
点评:本题考查了向量的数量积的运算,
•
=|
|•|
|cos<
,
>.
| a |
| b |
| a |
| b |
| a |
| b |

练习册系列答案
相关题目
已知各项均为正数的等比数列{an}中,a1a2a3=5,a7a8a9=10,则a4a5a6=( )
A、4
| ||
B、5
| ||
| C、6 | ||
| D、7 |
函数y=3-3x-
(x∈(0,+∞))的最大值是( )
| 1 |
| x |
| A、3 | ||
B、3-3
| ||
C、3-2
| ||
| D、-1 |
若两个等差数列{an}、{bn}的前项和分别为Sn、Tn,对任意的n∈N*都有
=
,则
+
的值是( )
| Sn |
| Tn |
| 2n-1 |
| 4n-3 |
| a4 |
| b5+b8 |
| a9 |
| b3+b10 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知sinα<0,tanα<0,则角α所在的象限是( )
| A、一 | B、二 | C、三 | D、四 |
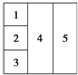 如图,用4种不同的颜色对图中5个区域涂色( 4种颜色全部使用 ),要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色方法有
如图,用4种不同的颜色对图中5个区域涂色( 4种颜色全部使用 ),要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色方法有