题目内容
已知在棱长为1的正方体ABCD-A1B1C1D1中,点M、N、P分别是棱AB、BC、AA1的中点,给出下列五个结论:
①AC⊥PM;
②B1D∥PMN;
③AC∥平面PMN;
④过P、M、N的平面截该正方体所得的截面面积为
;
⑤B1P⊥平面PMN.
以上结论中正确的是 .(写出所有正确结论的序号)
①AC⊥PM;
②B1D∥PMN;
③AC∥平面PMN;
④过P、M、N的平面截该正方体所得的截面面积为
3
| ||
| 4 |
⑤B1P⊥平面PMN.
以上结论中正确的是
考点:命题的真假判断与应用
专题:阅读型,空间位置关系与距离,空间角
分析:①由平行可知AC和CD1所成的角即为AC和PM所成的角,在等边三角形ACD1中,∠ACD1=60°,即可判断;
②运用线面垂直的判定和性质,即可证得B1D⊥平面PMN;
③运用线面平行的判定定理,即可得到;
④画出过P、M、N的平面截该正方体所得的截面为正六边形,边长为
,求出面积,即可判断;
⑤若B1P⊥平面PMN,又B1D⊥平面PMN,则B1D与B1P重合,即可判断.
②运用线面垂直的判定和性质,即可证得B1D⊥平面PMN;
③运用线面平行的判定定理,即可得到;
④画出过P、M、N的平面截该正方体所得的截面为正六边形,边长为
| ||
| 2 |
⑤若B1P⊥平面PMN,又B1D⊥平面PMN,则B1D与B1P重合,即可判断.
解答:
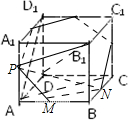 解:①∵PM∥A1B,A1B∥CD1,∴PM∥CD1,即AC和CD1所成的角即为AC和PM所成的角,在等边三角形ACD1中,∠ACD1=60°,故①错;
解:①∵PM∥A1B,A1B∥CD1,∴PM∥CD1,即AC和CD1所成的角即为AC和PM所成的角,在等边三角形ACD1中,∠ACD1=60°,故①错;
②∵AC⊥BD,AC⊥BB1,∴AC⊥平面BDB1,∴AC⊥B1D,即MN⊥B1D,
同理PM⊥B1D,则B1D⊥平面PMN,故②错;
③∵AC∥MN,AC?平面PMN,∴AC∥平面PMN,故③对;
④过P、M、N的平面截该正方体所得的截面为正六边形,如图所示,边长为
,
面积为6×
×(
)2=
,故④对;
⑤若B1P⊥平面PMN,又B1D⊥平面PMN,则B1D与B1P重合,故⑤错.
故答案为:③④
 解:①∵PM∥A1B,A1B∥CD1,∴PM∥CD1,即AC和CD1所成的角即为AC和PM所成的角,在等边三角形ACD1中,∠ACD1=60°,故①错;
解:①∵PM∥A1B,A1B∥CD1,∴PM∥CD1,即AC和CD1所成的角即为AC和PM所成的角,在等边三角形ACD1中,∠ACD1=60°,故①错;②∵AC⊥BD,AC⊥BB1,∴AC⊥平面BDB1,∴AC⊥B1D,即MN⊥B1D,
同理PM⊥B1D,则B1D⊥平面PMN,故②错;
③∵AC∥MN,AC?平面PMN,∴AC∥平面PMN,故③对;
④过P、M、N的平面截该正方体所得的截面为正六边形,如图所示,边长为
| ||
| 2 |
面积为6×
| ||
| 4 |
| ||
| 2 |
3
| ||
| 4 |
⑤若B1P⊥平面PMN,又B1D⊥平面PMN,则B1D与B1P重合,故⑤错.
故答案为:③④
点评:本题考查空间直线与平面的位置关系,主要是平行和垂直,记熟线面平行、垂直的判定和性质是迅速解题的关键,同时考查截面的画法及计算,以及空间异面直线所成的角的求法,属于基础题和易错题.

练习册系列答案
相关题目
已知各项均为正数的等比数列{an}中,a1a2a3=5,a7a8a9=10,则a4a5a6=( )
A、4
| ||
B、5
| ||
| C、6 | ||
| D、7 |
已知函数f(x)=
在R上为减函数,则实数a的取值范围是( )
|
| A、(0,1) | ||
B、(0,
| ||
C、(-∞,
| ||
D、(
|