题目内容
在△ABC中,已知tan
=sinC,则△ABC的形状为 .
| A+B |
| 2 |
考点:角的变换、收缩变换,半角的三角函数
专题:计算题,三角函数的求值
分析:由tan
=sinC,可得
=sinC,求出C,即可得出结论.
| A+B |
| 2 |
cos
| ||
sin
|
解答:
解:∵tan
=sinC,
∴
=sinC,
∴sin
=
,
∴
=45°,
∴C=90°,
∴△ABC是直角三角形.
故答案为:直角三角形.
| A+B |
| 2 |
∴
cos
| ||
sin
|
∴sin
| C |
| 2 |
| ||
| 2 |
∴
| C |
| 2 |
∴C=90°,
∴△ABC是直角三角形.
故答案为:直角三角形.
点评:本题考查三角函数的化简,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
下列叙述中正确的是( )
| A、若 p∧(¬q)为假,则一定是p假q真 |
| B、命题“?x∈R,x2≥0”的否定是“?x∈R,x2≥0” |
| C、若a,b,c∈R,则“ab2>cb2”的充分不必要条件是“a>c” |
| D、设α是一平面,a,b是两条不同的直线,若 a⊥α,b⊥α,则a∥b |
 如图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ω+φ)+b则在6≤x≤14时这段曲线的函数解析式是
如图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ω+φ)+b则在6≤x≤14时这段曲线的函数解析式是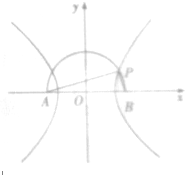 如图,在以点O为圆心,AB为直径的半圆中,P为半圆弧上一点,且AB=4,∠PAB=15°,若A、B分别为双曲线的左、右焦点,则双曲线的标准方程是
如图,在以点O为圆心,AB为直径的半圆中,P为半圆弧上一点,且AB=4,∠PAB=15°,若A、B分别为双曲线的左、右焦点,则双曲线的标准方程是