题目内容
函数y=-
的图象按向量
=(1,0)平移之后得到的函数图象与函数y=2sinπx(-2≤x≤4)的图象所有交点的橫坐标之和等于( )
| 1 |
| x |
| a |
| A、2 | B、4 | C、6 | D、8 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:压轴题,数形结合
分析:y1=
的图象由奇函数y=-
的图象向右平移1个单位而得,所以它的图象关于点(1,0)中心对称,再由正弦函数的对称中心公式,可得函数y2=2sinπx的图象的一个对称中心也是点(1,0),故交点个数为偶数,且每一对对称点的横坐标之和为2.由此不难得到正确答案.
| 1 |
| 1-x |
| 1 |
| x |
解答:
 解:函数y=-
解:函数y=-
的图象按向量
=(1,0)平移之后得到函数y1=
,y2=2sinπx的图象有公共的对称中心(1,0),作出两个函数的图象如图:
当1<x≤4时,y1<0,
而函数y2在(1,4)上出现1.5个周期的图象,
在(1,
)和(
,
)上是减函数;
在(
,
)和(
,4)上是增函数.
∴函数y1在(1,4)上函数值为负数,且与y2的图象有四个交点E、F、G、H,
相应地,y1在(-2,1)上函数值为正数,且与y2的图象有四个交点A、B、C、D,
且:xA+xH=xB+xG═xC+xF=xD+xE=2,故所求的横坐标之和为8,
故选:D.
 解:函数y=-
解:函数y=-| 1 |
| x |
| a |
| 1 |
| 1-x |
当1<x≤4时,y1<0,
而函数y2在(1,4)上出现1.5个周期的图象,
在(1,
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
在(
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
∴函数y1在(1,4)上函数值为负数,且与y2的图象有四个交点E、F、G、H,
相应地,y1在(-2,1)上函数值为正数,且与y2的图象有四个交点A、B、C、D,
且:xA+xH=xB+xG═xC+xF=xD+xE=2,故所求的横坐标之和为8,
故选:D.
点评:发现两个图象公共的对称中心是解决本题的入口,讨论函数y2=2sinπx的单调性找出区间(1,4)上的交点个数是本题的难点所在.

练习册系列答案
相关题目
记{x}表示不超过x的最大整数,函数f(x)=
-
,在x>0时,恒有[f(x)]=0,则实数a的取值范围是( )
| ax |
| 1+ax |
| 1 |
| 2 |
| A、a>1 | ||
| B、0<a<1 | ||
C、a>
| ||
D、0<a<
|
设函数f(x)=log2(x2-4x+a)(a>4),若所有点(s,f(t))(s,t∈[1,3])构成一个正方形区域,则函数f(x)的单调增区间为( )
| A、[1,2] |
| B、[2,3] |
| C、(-∞,2] |
| D、[2,+∞) |
已知实数x,y满足
,若z=
的最大值为
,则a的值是( )
|
| ay |
| 3(x+1) |
| 1 |
| 8 |
| A、1 | ||
| B、-1 | ||
C、-
| ||
D、
|
在复平面内,复数z=
对应的点位于( )
| 2i |
| -1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
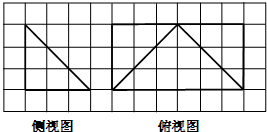 如图,网格纸的各小格都是正方形,粗实线画出的是一个锥体的侧视图和俯视图,则该锥体的正视图可能是( )
如图,网格纸的各小格都是正方形,粗实线画出的是一个锥体的侧视图和俯视图,则该锥体的正视图可能是( )