题目内容
如图是一个四棱锥的三视图，则该四棱锥的体积是 ．
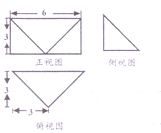
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知的三视图可得：该几何体是一个以主视图为底面的四棱锥，分别求出底面面积和高，代入棱锥体积公式，可得答案．
解答：
解：由已知的三视图可得：该几何体是一个以主视图为底面的四棱锥，
其底面面积S=3×6=18，
高h=3，
故体积V=
Sh=
×18×3=18，
故答案为：18
其底面面积S=3×6=18，
高h=3，
故体积V=
| 1 |
| 3 |
| 1 |
| 3 |
故答案为：18
点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
将函数f（x）=sin2x的图象向右平移
个单位，得到函数y=g（x）的图象，则它的一个对称中心是（ ）
| π |
| 6 |
A、（-
| ||
B、（-
| ||
C、（
| ||
D、（
|
若函数y=cos（
+θ）（0＜θ＜2π）在区间（-π，π）上单调递增，则实数θ的取值范围是（ ）
| x |
| 3 |
A、[0，
| ||||
| B、[π，2π] | ||||
C、[
| ||||
D、[
|
函数f（x）=ln（2x-1）+
的定义域为（ ）
| 1-x |
A、（
| ||
B、[
| ||
| C、（-∞，1） | ||
D、（
|
“φ=
”是“函数y=sin（x+2φ）是偶函数”的（ ）
| π |
| 4 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分又不必要条件 |
复数m2-1+（m+1）i是纯虚数，则实数m的值为（ ）
| A、-1 | B、1 | C、±1 | D、±2 |
已知函数f（x）=
，则f（3）=（ ）
|
A、-
| ||
B、
| ||
C、-
| ||
D、
|