Question

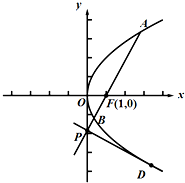抛物线C：y²=2px（p＞0），过抛物线C的焦点F（1，0）的直线l与抛物线交于A，B两点，交y轴于点P．
（1）求证：|PF|²=|PA|•|PB|；
（2）过P作抛物线C的切线，切点为D（异于原点），是否存在常数λ，使得

1

kDA

+

1

kDB

=

λ

kDF

恒成立？

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）设P（0，m），A（x₁，y₁），B（x₂，y₂），F（1，0）．则直线l的方程为x+

y

m

=1，化为
y=m（1-x），与抛物线的方程联立化为m²x²-（2m²+4）x+m²=0，利用根与系数的关系、两点之间的距离公式即可得出．
（2）假设设D(x0，-2

x0

)，取y=-2

x

，则y′=-

1

x

，利用斜率计算公式和导数的几何意义可得：

x0

=-m．由（1）可得

x1

-

x2

=

x1+x2-2 x1x2

=-

2

m

．再利用斜率计算公式可得：k_DF=

2m

m2-1

，
k_DA=

2

x1 - x0

，k_DB=

-2

x2 + x0

．得到k_DF•(

1

kDA

+

1

kDB

)=

2m

m2-1

•

x1 - x2 -2 x0

2

=2．即可得出．

解答： （1）证明：设P（0，m），A（x₁，y₁），B（x₂，y₂），F（1，0）．
则直线l的方程为x+

y

m

=1，化为y=m（1-x），
联立

y=m(1-x) y2=4x

，化为m²x²-（2m²+4）x+m²=0，
∴x₁+x₂=2+

4

m2

，x₁x₂=1．
∴|PF|²=1+m²，
|PA||PB|=

x 2 1 +(y1-m)2

x 2 2 +(y2-m)2

=

x 2 1 +m2 x 2 1

x 2 2 +m2 x 2 2

=（1+m²）

(x1x2)2

=1+m²．
∴|PF|²=|PA|•|PB|．
（2）解：假设设D(x0，-2

x0

)，取y=-2

x

，则y′=-

1

x

，
∴切线PD的斜率=-

1

x0

=

-2 x0 -m

x0

，化为

x0

=-m．
∴

x1

-

x2

=

x1+x2-2 x1x2

=

2+ 4 m2 -2

=-

2

m

．
∴k_DF=

-2 x0

x0-1

=

2m

m2-1

，
k_DA=

2 x1 +2 x0

x1-x0

=

2

x1 - x0

，k_DB=

-2 x2 +2 x0

x2-x0

=

-2

x2 + x0

．
∴k_DF•(

1

kDA

+

1

kDB

)=

2m

m2-1

•

x1 - x2 -2 x0

2

=

2m

m2-1

•

-2 m +2m

2

=2．
∴存在常数λ=2，使得

1

kDA

+

1

kDB

=

λ

kDF

恒成立．

点评：本题考查了直线与抛物线相交相切问题转化为方程联立可得根与系数的关系、利用导数研究切线问题、斜率计算公式，考查了推理能力和计算能力，属于难题．