题目内容
已知f(x)=ln(x+1),g(x)=
ax2+bx.
(1)若b=2,且h(x)=f(x-1)-g(x)存在单调递减区间,求a的取值范围;
(2)若a=0,b=1时,求证f(x)-g(x)≤0对于x∈(-1,+∞)成立.
| 1 |
| 2 |
(1)若b=2,且h(x)=f(x-1)-g(x)存在单调递减区间,求a的取值范围;
(2)若a=0,b=1时,求证f(x)-g(x)≤0对于x∈(-1,+∞)成立.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:(1)求出导数,问题等价于h′(x)=
-ax-2<0在(0,+∞)有解,分离参数求出函数的最小值即可;
(2)令h(x)=f(x)-g(x)=ln(x+1)-x,求出h(x)的表达式,求出导数,求得h(x)的最大值即可得证.
| 1 |
| x |
(2)令h(x)=f(x)-g(x)=ln(x+1)-x,求出h(x)的表达式,求出导数,求得h(x)的最大值即可得证.
解答:
(1)解:∵函数h(x)=lnx-
ax2-2x的定义域为(0,+∞),
且函数h(x)存在单调递减区间,
∴h′(x)=
-ax-2<0在(0,+∞)有解,
即-ax2-2x+1<0在(0,+∞)有解,
故a>
-
=(
-1)2-1在(0,+∞)有解,
∴a>-1,
故a的范围为(-1,+∞).
(2)证明:若a=0,b=1时,令h(x)=f(x)-g(x)=ln(x+1)-x,
则h′(x)=
-1=
,
当x>0时,h′(x)<0,h(x)单调递减;当-1<x<0时,h′(x)>0,h(x)单调递增.
则x=0为极大值点,也为最大值点,
故最大值为h(0)=0,
故h(x)≤h(0).
即有f(x)-g(x)≤0对于x∈(-1,+∞)成立.
| 1 |
| 2 |
且函数h(x)存在单调递减区间,
∴h′(x)=
| 1 |
| x |
即-ax2-2x+1<0在(0,+∞)有解,
故a>
| 1 |
| x2 |
| 2 |
| x |
| 1 |
| x |
∴a>-1,
故a的范围为(-1,+∞).
(2)证明:若a=0,b=1时,令h(x)=f(x)-g(x)=ln(x+1)-x,
则h′(x)=
| 1 |
| x+1 |
| -x |
| x+1 |
当x>0时,h′(x)<0,h(x)单调递减;当-1<x<0时,h′(x)>0,h(x)单调递增.
则x=0为极大值点,也为最大值点,
故最大值为h(0)=0,
故h(x)≤h(0).
即有f(x)-g(x)≤0对于x∈(-1,+∞)成立.
点评:本题考查导数的运用:求单调区间和求极值、最值,注意存在与恒成立的区别,属于中档题.

练习册系列答案
相关题目

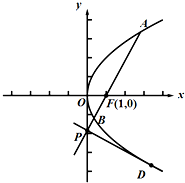 抛物线C:y2=2px(p>0),过抛物线C的焦点F(1,0)的直线l与抛物线交于A,B两点,交y轴于点P.
抛物线C:y2=2px(p>0),过抛物线C的焦点F(1,0)的直线l与抛物线交于A,B两点,交y轴于点P. 中国首届绿色运动会2011年10月18日至11月2日在安徽池州举行.绿运会期间,“上海城”举办了绿色产品展销会,并在展销会场设有购物满50元就获得一次有奖摸球活动.一个不透明的袋子中装有大小相同的8个球,其中标有1,2,3,4数字的球各2个,现从中任意抽取2个,用ξ表示抽取的这两个球上的数字之和.求:
中国首届绿色运动会2011年10月18日至11月2日在安徽池州举行.绿运会期间,“上海城”举办了绿色产品展销会,并在展销会场设有购物满50元就获得一次有奖摸球活动.一个不透明的袋子中装有大小相同的8个球,其中标有1,2,3,4数字的球各2个,现从中任意抽取2个,用ξ表示抽取的这两个球上的数字之和.求: