题目内容
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(1)求证平面AEC⊥平面PDB;
(2)当PD=
AB,且E为PB中点时,求AE与平面PDB所成角的正切值.
(1)求证平面AEC⊥平面PDB;
(2)当PD=
| 3 |
考点:直线与平面所成的角,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)要证明面面垂直首先要通过线面垂直来进行转化,然后找到线面垂直的充分条件即可.
(2)要求直线与平面的夹角,可以在线上找到一点作面的垂线,然后通过解三角形知识求解.
(2)要求直线与平面的夹角,可以在线上找到一点作面的垂线,然后通过解三角形知识求解.
解答:
证明:如图所示:
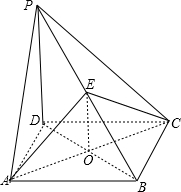
连接AC,BD交于O,ABCD的底面是正方形,
∴AC⊥BD,
∵四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD AC?平面ABCD,
∴PD⊥AC,
PD∩BD=D,
∴AC⊥平面PBD,
∵AC?平面ACE,
∴平面AEC⊥平面PDB;
(2)由于E为PB中点,连接OE,
由(1)得OE⊥AC,OE⊥BD,
∴∠EAC就是AE与平面PDB所成角,
设AB=1 PD=
AB,
PD=
,
∴AC=
AO=
OE=
,
在Rt△AOE中,tan∠AEO=
=
,
AE与平面PDB所成角的正切值为
.

连接AC,BD交于O,ABCD的底面是正方形,
∴AC⊥BD,
∵四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD AC?平面ABCD,
∴PD⊥AC,
PD∩BD=D,
∴AC⊥平面PBD,
∵AC?平面ACE,
∴平面AEC⊥平面PDB;
(2)由于E为PB中点,连接OE,
由(1)得OE⊥AC,OE⊥BD,
∴∠EAC就是AE与平面PDB所成角,
设AB=1 PD=
| 3 |
PD=
| 3 |
∴AC=
| 2 |
| ||
| 2 |
| ||
| 2 |
在Rt△AOE中,tan∠AEO=
| ||||
|
| ||
| 3 |
AE与平面PDB所成角的正切值为
| ||
| 3 |
点评:本题考查的知识点:直线与平面垂直的性质定理,直线与平面垂直的判定定理,直线与平面的夹角,解直角三角形知识,是高考的重点题型.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
直线ρcosθ=2关于直线θ=
对称的直线方程为( )
| π |
| 4 |
| A、ρcosθ=-2 |
| B、ρsinθ=2 |
| C、ρsinθ=-2 |
| D、ρ=2sinθ |