题目内容
已知函数f(x)=x2-(c+1)x+c(c∈R).
(1)解关于x的不等式f(x)<0;
(2)当c=-2时,不等式f(x)>ax-5在(0,2)上恒成立,求实数a的取值范围.
(1)解关于x的不等式f(x)<0;
(2)当c=-2时,不等式f(x)>ax-5在(0,2)上恒成立,求实数a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)根据题意,由f(x)<0,解含有参数的不等式x2-(c+1)x+c<0;讨论c的取值,求出不等式的解集.
(2)利用分离变量的方法求a的取值范围.
(2)利用分离变量的方法求a的取值范围.
解答:
解:∵f(x)<0,
∴x2-(c+1)x+c=(x-1)(x-c)<0;
∴①当c<1时,c<x<1,
②当c=1时,(x-1)2<0,∴x∈∅,
③当c>1时,1<x<c,
综上,当c<1时,不等式的解集为{x|c<x<1},
当c=1时,不等式的解集为∅,
当c>1时,不等式的解集为{x|1<x<c}.
(2)把c=-2时,f(x)>ax-5,由于x∈(0,2),
所以不等式可化为:a<
=x+
+1,
因为x+
+3≥2
+1=2
+1,
所以a<2
+1.
∴x2-(c+1)x+c=(x-1)(x-c)<0;
∴①当c<1时,c<x<1,
②当c=1时,(x-1)2<0,∴x∈∅,
③当c>1时,1<x<c,
综上,当c<1时,不等式的解集为{x|c<x<1},
当c=1时,不等式的解集为∅,
当c>1时,不等式的解集为{x|1<x<c}.
(2)把c=-2时,f(x)>ax-5,由于x∈(0,2),
所以不等式可化为:a<
| x2+x+3 |
| x |
| 3 |
| x |
因为x+
| 3 |
| x |
x•
|
| 3 |
所以a<2
| 3 |
点评:本题考查了求含有参数的一元二次不等式的解集问题,解题时应讨论c的取值,对不等式解集的影响,是易错题;方法求参数的取值范围经常用分离变量的方法.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
若
<
<0,则下列结论不正确的是( )
| 1 |
| a |
| 1 |
| b |
| A、a2<b2 | ||||
| B、ab<b2 | ||||
| C、|a|+|b|>|a+b| | ||||
D、
|
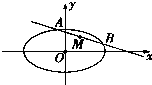 如图,
如图,