题目内容
已知a，b，c＞0，a+b+c=1，求证：（a+
）（b+
）（c+
）≥
．
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1000 |
| 27 |
考点：基本不等式在最值问题中的应用
专题：证明题,不等式的解法及应用
分析：左边=abc+（
+
+
）+（
+
+
）+
≥abc+
+3
+
=(
+
)3，构造函数f（x）=(x+
)3（x∈（0，
]），证明函数在（0，
]上单调递减，即可证明结论．
| bc |
| a |
| ac |
| b |
| ab |
| c |
| c |
| ab |
| b |
| ac |
| a |
| bc |
| 1 |
| abc |
| 1 |
| abc |
| 3 | abc |
| 3 | |||
|
| 3 | abc |
| 1 | |||
|
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
解答：
证明：左边=abc+（
+
+
）+（
+
+
）+
≥abc+
+3
+
=(
+
)3
构造函数f（x）=(x+
)3（x∈（0，
]），
则f′（x）=3(x+
)2(1-
)＜0，
∴函数在（0，
]上单调递减，
∴函数f（x）=(x+
)3（x∈（0，
]）的最小值为
，
∴(
+
)3的最小值为
，
∴（a+
）（b+
）（c+
）≥
．
| bc |
| a |
| ac |
| b |
| ab |
| c |
| c |
| ab |
| b |
| ac |
| a |
| bc |
| 1 |
| abc |
| 1 |
| abc |
| 3 | abc |
| 3 | |||
|
| 3 | abc |
| 1 | |||
|
构造函数f（x）=(x+
| 1 |
| x |
| 1 |
| 3 |
则f′（x）=3(x+
| 1 |
| x |
| 1 |
| x2 |
∴函数在（0，
| 1 |
| 3 |
∴函数f（x）=(x+
| 1 |
| x |
| 1 |
| 3 |
| 1000 |
| 27 |
∴(
| 3 | abc |
| 1 | |||
|
| 1000 |
| 27 |
∴（a+
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1000 |
| 27 |
点评：本题考查基本不等式在最值问题中的应用，考查导数知识，考查学生分析解决问题的能力，有难度．
练习册系列答案
春雨教育同步作文系列答案
相关题目
乘积5×6×7×…×20等于（ ）
A、A
| ||
B、A
| ||
C、A
| ||
D、A
|
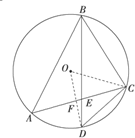如图，⊙O是△ABC的外接圆，D是 