题目内容
已知抛物线y2=-4x的焦点为F,其准线与x轴交于点M,过M作斜率为K的直线l与抛物线交于A、B两点,弦AB的中点为P,AB的垂直平分线与x轴交于E(x0,0).
(1)求k的取值范围;
(2)求证:x0<-3;
(3)△PEF能否成为以EF为底的等腰三角形?若能,求此k的值;若不能,请说明理由.
(1)求k的取值范围;
(2)求证:x0<-3;
(3)△PEF能否成为以EF为底的等腰三角形?若能,求此k的值;若不能,请说明理由.
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意求出抛物线的准线方程,求出M的坐标,写出直线方程的点斜式,和抛物线方程联立后由判别式等于0得答案;
(2)利用一元二次方程的根与系数关系求出AB中点P的坐标,代入直线方程求P得纵坐标,写出AB的垂直平分线方程,求出与x轴交于E的坐标,由(1)中求得的k的范围得到x0<-3;
(3)若△PEF能成为以EF为底的等腰三角形,则EF中点的横坐标与P的横坐标相等,由此列式求得k的值.
(2)利用一元二次方程的根与系数关系求出AB中点P的坐标,代入直线方程求P得纵坐标,写出AB的垂直平分线方程,求出与x轴交于E的坐标,由(1)中求得的k的范围得到x0<-3;
(3)若△PEF能成为以EF为底的等腰三角形,则EF中点的横坐标与P的横坐标相等,由此列式求得k的值.
解答:
(1)解:由题意,M(1,0),
设斜率为k的直线方程为y=k(x-1),
代入抛物线方程,整理可得k2x2-(2k2-4)x+k2=0.
∵过M作斜率为k的直线与抛物线交于A、B两点,
∴(2k2-4)2-4k4>0且k≠0,
∴-1<k<0或0<k<1.
∴k的取值范围是(-1,0)∪(0,1);
(2)证明:由(1)知,k2x2-(2k2-4)x+k2=0.
∵过M作斜率为k的直线与抛物线交于A、B两点,弦AB的中点为P.
∴P的横坐标为
,
代入y=k(x-1),可得P的纵坐标为-
.
∴AB的垂直平分线方程为y+
=-
(x-
).
令y=0,可得x=-1-
.
∵-1<k<0或0<k<1,
∴k2<1且k≠0,
∴
>2,
∴1+
>3,即x0<-3;
(3)若△PEF能成为以EF为底的等腰三角形,则
由EF中点的横坐标与P的横坐标相等,可得
=
,
∴2k2=1.
即k=±
.
故△PEF能成为以EF为底的等腰三角形,此时k=±
.
设斜率为k的直线方程为y=k(x-1),
代入抛物线方程,整理可得k2x2-(2k2-4)x+k2=0.
∵过M作斜率为k的直线与抛物线交于A、B两点,
∴(2k2-4)2-4k4>0且k≠0,
∴-1<k<0或0<k<1.
∴k的取值范围是(-1,0)∪(0,1);
(2)证明:由(1)知,k2x2-(2k2-4)x+k2=0.
∵过M作斜率为k的直线与抛物线交于A、B两点,弦AB的中点为P.
∴P的横坐标为
| k2-2 |
| k2 |
代入y=k(x-1),可得P的纵坐标为-
| 2 |
| k |
∴AB的垂直平分线方程为y+
| 2 |
| k |
| 1 |
| k |
| k2-2 |
| k2 |
令y=0,可得x=-1-
| 2 |
| k2 |
∵-1<k<0或0<k<1,
∴k2<1且k≠0,
∴
| 2 |
| k2 |
∴1+
| 2 |
| k2 |
(3)若△PEF能成为以EF为底的等腰三角形,则
由EF中点的横坐标与P的横坐标相等,可得
-1-1-
| ||
| 2 |
| k2-2 |
| k2 |
∴2k2=1.
即k=±
| ||
| 2 |
故△PEF能成为以EF为底的等腰三角形,此时k=±
| ||
| 2 |
点评:本题考查了抛物线的性质,考查了直线与抛物线的关系,综合考查了学生灵活运用抛物线的性质求解问题的能力,是高考试卷中的压轴题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若正数x,y满足
+
=1,则3x+4y的最小值是( )
| 3 |
| 5x |
| 1 |
| 5y |
A、
| ||
| B、5 | ||
C、
| ||
| D、6 |
下列函数与y=x是相同函数的是( )
A、y=
| ||
B、y=(
| ||
| C、y=lnex | ||
| D、y=elnx |
若变量x,y满足约束条件
,则z=2x+y的最大值为( )
|
| A、1 | B、-1 | C、-2 | D、-4 |
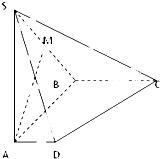 如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,AD∥BC,∠ABC=90°,SA=AB=BC=2,AD=1.M是棱SB的中点.
如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,AD∥BC,∠ABC=90°,SA=AB=BC=2,AD=1.M是棱SB的中点. 如图,AB是圆O的直径,C是圆O上的点.P是圆所在的面外一点.设Q为PA的中点,G为AOC的重心.求证:QG∥平面PBC.
如图,AB是圆O的直径,C是圆O上的点.P是圆所在的面外一点.设Q为PA的中点,G为AOC的重心.求证:QG∥平面PBC.