题目内容
已知函数f(x)=|x-a|+2x,a∈R.
(Ⅰ)当a=2时,解不等式f(x)≥4x+2的解集;
(Ⅱ)若存在x使f(x)≤-|x+2|+2x+1成立,求a的取值范围.
(Ⅰ)当a=2时,解不等式f(x)≥4x+2的解集;
(Ⅱ)若存在x使f(x)≤-|x+2|+2x+1成立,求a的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)当a=2时,|x-2|+2x≥4x+2?|x-2|≥2x+2,对x分x-2≥0与x-2<0讨论,去掉绝对值符号,即可求得不等式f(x)≥4x+2的解集;
(Ⅱ)利用绝对值不等式|x-a|+|x+2|≥|x+2-x+a|=|a+2|及不等式|x-a|+|x+2|≤1即可求得a的取值范围.
(Ⅱ)利用绝对值不等式|x-a|+|x+2|≥|x+2-x+a|=|a+2|及不等式|x-a|+|x+2|≤1即可求得a的取值范围.
解答:
解:(Ⅰ)当a=2时,|x-2|+2x≥4x+2,
即|x-2|≥2x+2,
∴
或
,
∴
或
,
∴x≤0,即不等式的解集为{x|x≤0}…5分
(Ⅱ)若存在x使f(x)≤-|x+2|+2x+1 成立,即存在x使|x-a|+|x+2|≤1 成立,
∵|x-a|+|x+2|≥|x+2-x+a|=|a+2|,
∴|a+2|≤1,
∴-3≤a≤-1…10分
即|x-2|≥2x+2,
∴
|
|
∴
|
|
∴x≤0,即不等式的解集为{x|x≤0}…5分
(Ⅱ)若存在x使f(x)≤-|x+2|+2x+1 成立,即存在x使|x-a|+|x+2|≤1 成立,
∵|x-a|+|x+2|≥|x+2-x+a|=|a+2|,
∴|a+2|≤1,
∴-3≤a≤-1…10分
点评:本题考查含绝对值的不等式的解法,通过分类讨论,去掉绝对值符号是解决问题的关键,着重考查等价转化思想与运算求解能力,属于中档题.

练习册系列答案
相关题目
给定命题p:函数y=ln
为奇函数;命题q:函数y=
为偶函数,下列说法正确的是( )
| 1-x |
| x+1 |
| ex-1 |
| ex+1 |
| A、p∨q是假命题 |
| B、¬p∧q是假命题 |
| C、p∧q是真命题 |
| D、¬p∨q是真命题 |
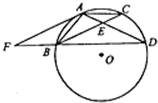 如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=
如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=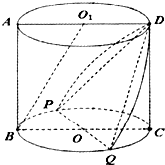 在如图所示的圆柱OO1中,过轴OO1作截面ABCD.已知PQ是圆O异于BC的直径.
在如图所示的圆柱OO1中,过轴OO1作截面ABCD.已知PQ是圆O异于BC的直径.