Question

4．四面体ABCD的四个顶点都在球O的球面上，AB⊥平面BCD，△BCD是边长为3的等边三角形，若AB=2，则球O的表面积为16π．

Answer 1

分析 取CD的中点E，连结AE，BE，作出外接球的球心，求出半径，即可求出表面积．

解答 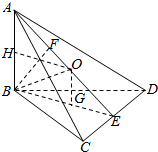解：取CD的中点E，连结AE，BE，∵在四面体ABCD中，AB⊥平面BCD，
△BCD是边长为3的等边三角形．
∴Rt△ABC≌Rt△ABD，△ACD是等腰三角形，
△BCD的中心为G，作OG∥AB交AB的中垂线HO于O，O为外接球的中心，
BE=$\frac{3\sqrt{3}}{2}$，BG=$\sqrt{3}$，
R=$\sqrt{3+1}$=2．
四面体ABCD外接球的表面积为：4πR²=16π．
故答案为：16π．

点评 本题考查球的内接体知识，考查空间想象能力，确定球的切线与半径是解题的关键．