题目内容
9.已知直线l的方程为y=kx-1,圆的方程为x2+y2-2x+4y+4=0.若直线l与圆相交截得的弦长为$\sqrt{3}$,求直线l的斜率k.分析 由半径的平方等于圆心到直线的距离平方与弦长一半的平方的和求出圆心到直线的距离,再建立方程求解.
解答 解:圆的方程为x2+y2-2x+4y+4=0,可化为(x-1)2+(y+2)2=1,圆心坐标为(1,-2),半径为1.
∵直线l与圆相交截得的弦长为$\sqrt{3}$,
∴圆心到直线的距离为d=$\sqrt{1-(\frac{\sqrt{3}}{2})^{2}}$=$\frac{1}{2}$,
∴$\frac{|k+1|}{\sqrt{{k}^{2}+1}}$=$\frac{1}{2}$,
解得k=$\frac{-4±\sqrt{7}}{3}$,
故直线方程为y=$\frac{-4±\sqrt{7}}{3}$x-1.
点评 本题主要考查直线方程,考查直线与圆的位置关系,在相交时半径的平方等于圆心到直线的距离平方与弦长一半的平方的和的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.为了增强环保意识,我校从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:
(Ⅰ)试判断是否有99%的把握认为环保知识是否优秀与性别有关;
(Ⅱ)为参加市里举办的环保知识竞赛,学校举办预选赛,已知在环保测试中优秀的同学通过预选赛的概率为$\frac{2}{3}$,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X表示这3人中通过预选赛的人数,求X的分布列与数学期望.
附:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| 优秀 | 非优秀 | 总计 | |
| 男生 | 40 | 20 | 60 |
| 女生 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
(Ⅱ)为参加市里举办的环保知识竞赛,学校举办预选赛,已知在环保测试中优秀的同学通过预选赛的概率为$\frac{2}{3}$,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X表示这3人中通过预选赛的人数,求X的分布列与数学期望.
附:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
| k | 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
14.若函数y=f(x)在x=a处的导数为A,则$\underset{lim}{△x→0}$$\frac{f(a+△x)-f(a-△x)}{△x}$为( )
| A. | A | B. | 2A | C. | $\frac{A}{2}$ | D. | 0 |
19.当x=$\frac{π}{4}$时,函数f(x)=sin(x+φ)取得最小值,则函数y=f($\frac{3π}{4}$-x)的一个单调递增区间是( )
| A. | (0,$\frac{π}{2}$) | B. | ($\frac{π}{2}$,π) | C. | (-$\frac{π}{2}$,-$\frac{π}{4}$) | D. | ($\frac{3π}{2}$,2π) |
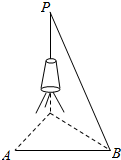 如图所示,要测量河对岸一电视塔的高PC,在河旁取A、B两点,测得AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°.
如图所示,要测量河对岸一电视塔的高PC,在河旁取A、B两点,测得AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°.