题目内容
某班50位学生体育成绩的频率分布表如下:
(Ⅰ)估计成绩不低于80分的概率;
(Ⅱ)从成绩不低于80分的学生中随机选取3人,该3人中成绩在90分以上(含90分)的人数记为ξ,求ξ的数学期望.
| 分数 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频率 | 0.06 | 0.12 | 0.58 | X | 0.06 |
(Ⅱ)从成绩不低于80分的学生中随机选取3人,该3人中成绩在90分以上(含90分)的人数记为ξ,求ξ的数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)由题设条件求出x=0.18,由此能估计出成绩不低于80分的概率.
(Ⅱ)由题意知ξ的取值可能为0,1,2,3,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的数学期望.
(Ⅱ)由题意知ξ的取值可能为0,1,2,3,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的数学期望.
解答:
解:(Ⅰ)由题意得:
0.06+0.12+0.58+x+0.06=1,
∴x=0.18,
∴估计成绩不低于80分的概率为:
0.18+0.06=0.24.
(Ⅱ)由题意知:
成绩在[80,90)之间的学生有50×0.18=9(人),
成绩在[90,100]之间的学生有50×0.06=3(人),
从成绩不低于80分的学生中随机选取3人,
该3人中成绩在90分以上(含90分)的人数ξ的取值可能为0,1,2,3,
P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
,
∴ξ的分布列为:
∴ξ的数学期望Eξ=0×
+1×
+2×
+3×
=
.
0.06+0.12+0.58+x+0.06=1,
∴x=0.18,
∴估计成绩不低于80分的概率为:
0.18+0.06=0.24.
(Ⅱ)由题意知:
成绩在[80,90)之间的学生有50×0.18=9(人),
成绩在[90,100]之间的学生有50×0.06=3(人),
从成绩不低于80分的学生中随机选取3人,
该3人中成绩在90分以上(含90分)的人数ξ的取值可能为0,1,2,3,
P(ξ=0)=
| ||
|
| 21 |
| 55 |
P(ξ=1)=
| ||||
|
| 27 |
| 55 |
P(ξ=2)=
| ||||
|
| 27 |
| 220 |
P(ξ=3)=
| ||
|
| 1 |
| 220 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 21 |
| 55 |
| 27 |
| 55 |
| 27 |
| 220 |
| 1 |
| 220 |
| 3 |
| 4 |
点评:本题考查频率分布表的应用,考查离散型随机变量的数学期,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
“a=-7”是“直线(3+a)x+4y=5-3a与直线2x+(5+a)y=8互相平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
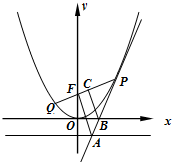 已知抛物线C:x2=4y的焦点为F,P是抛物线上异于原点的任意一点,直线PF与抛物线另一交点为点Q,设l是过点P的抛物线的切线,l与直线y=-1和x轴的交点分别为A,B.
已知抛物线C:x2=4y的焦点为F,P是抛物线上异于原点的任意一点,直线PF与抛物线另一交点为点Q,设l是过点P的抛物线的切线,l与直线y=-1和x轴的交点分别为A,B.