题目内容
如图，函数y=f（x）的图象在点P处的切线方程是y=kx+b，若f（1）-f′（1）=2，则b=（ ）
| A、-1 | B、1 | C、2 | D、-2 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：由图象可得P为切点，则由导数的几何意义可知f′（1）=k，又f（1）=k+b，即可得到b的值．
解答：
解：由于函数y=f（x）的图象在点P处的切线方程是y=kx+b，
且P（1，f（1）），
则f（1）=k+b，f′（1）=k，
由f（1）-f′（1）=2，得b=2，
故选C．
且P（1，f（1）），
则f（1）=k+b，f′（1）=k，
由f（1）-f′（1）=2，得b=2，
故选C．
点评：本题考查导数的几何意义：曲线在该点处的切线的斜率，考查基本的运算能力，属于基础题．
练习册系列答案
相关题目
过双曲线
-
=1（a＞0，b＞0）的右顶点A作斜率为-1的直线，该直线与双曲线的两条渐近线的交点分别为B，C．若
=
，则双曲线的渐近线方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| 1 |
| 2 |
| BC |
| A、3x±y=0 |
| B、x±3y=0 |
| C、2x±y=0 |
| D、x±2y=0 |
在平行四边形ABCD中，
+
-
等于（ ）
| BC |
| CD |
| AD |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知
=（4，2），
=（3，4），则△ABC的面积为（ ）
| AB |
| AC |
| A、5 | B、7.5 | C、10 | D、15 |
记者要为5名志愿者和他们帮助的2位老人拍照，要求排成一排，2位老人不相邻且不排在两端，不同的排法共有（ ）
| A、720种 | B、960种 |
| C、1440种 | D、480种 |
在边长为2的正三角形ABC中，设
=
，
=
，
=
，则
•
+
•
+
•
等于（ ）
| AB |
| a |
| BC |
| b |
| CA |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
| A、12 | B、-12 | C、6 | D、-6 |
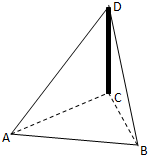如图所示，哈三中甲，乙两位同学分别站在新校区体育场内的A，B两点，利用三角函数知识测量锅炉房烟囱CD的高．已知AB=15米，∠DAC=60°，∠CAB=15°，∠CBA=45°，求烟囱CD的高．