题目内容
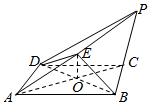
19. 如图,在四棱锥P-ABCD中,底面ABCD为正方形,点E是棱PA的中点,PB=PD,平面BDE⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,点E是棱PA的中点,PB=PD,平面BDE⊥平面ABCD.(Ⅰ)求证:PC∥平面BDE;
(Ⅱ)求证:PC⊥平面ABCD;
(Ⅲ) 设PC=λAB,试判断平面PAD⊥平面PAB能否成立;若成立,写出λ的一个值(只需写出结论).
分析 (Ⅰ)设AC∩BD=O,连接OE,推导出EO∥PC,由此能证明PC∥平面BDE.
(Ⅱ)法一:推导出△PAB≌△PAD,EO⊥BD,从而EO⊥平面ABCD,进而EO⊥AC,EO⊥BD,由此得到PC⊥AC,PC⊥BD,从而能证明PC⊥平面ABCD.
法二:连接PO,推导出BD⊥AC,PO⊥BD,从而BD⊥平面PAC,进而BD⊥OE,由此得到EO⊥平面ABCD,从而EO⊥AC,EO⊥BD,进而PC⊥AC,PC⊥BD,由此能证明PC⊥平面ABCD.
(Ⅲ) 由PC=λAB,得到平面PAD⊥平面PAB不能成立.
解答 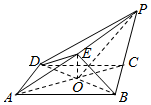
 (本小题9分)
(本小题9分)
证明:(Ⅰ)设AC∩BD=O,连接OE,
因为底面ABCD为正方形,所以O是AC的中点,又点E是棱PA的中点,
所以EO是的△PAC中位线,所以EO∥PC,…(1分)
因为EO?平面BDE,PC?平面BDE,
所以PC∥平面BDE. …(3分)
(Ⅱ)证法一:在△PAB和△PAD中,
因为AB=AD,PB=PD,PA=PA,
所以△PAB≌△PAD,又点E是棱PA的中点,
所以EB=ED,…(5分)所以EO⊥BD,
因为平面BDE⊥平面ABCD,平面BDE∩平面ABCD=BD,EO?平面BDE
所以EO⊥平面ABCD,…(7分)所以EO⊥AC,EO⊥BD,
因为EO∥PC,所以PC⊥AC,PC⊥BD,又AC∩BD=O
所以PC⊥平面ABCD. …(8分)
证法二:连接PO,因为底面ABCD是正方形,
所以O是BD的中点,BD⊥AC,又PB=PD,所以PO⊥BD,
又PO∩AC=O,PO?平面PAC,AC?平面PAC
所以BD⊥平面PAC
又OE?平面PAC,所以BD⊥OE,…(5分)
因为平面BDE⊥平面ABCD,平面BDE∩平面ABCD=BD,EO?平面BDE
所以EO⊥平面ABCD,…(7分)所以EO⊥AC,EO⊥BD,
因为OE∥PC,所以PC⊥AC,PC⊥BD,又AC∩BD=O
所以PC⊥平面ABCD. …(8分)
(Ⅲ) 不能成立. …(9分)
点评 本题考查线面平行、线面垂直的证明,考查两平面能否垂直的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方思想、数形结合思想,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | y=sin(2x-$\frac{5π}{6}$) | B. | y=sin(2x-$\frac{7π}{6}$) | C. | y=sin(2x-$\frac{π}{3}$) | D. | y=sin(2x+$\frac{2π}{3}$) |
| A. | $\sqrt{5}$ | B. | $±\sqrt{5}$ | C. | 3 | D. | ±3 |
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | -$\frac{{\sqrt{2}}}{2}$ |
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
| A. | m=1或m=-2 | B. | m=1 | C. | m=-2 | D. | m的值不存在 |